… or “The Traveling Salesman Problem is Not That Hard”.
When I talk to people about what I do for a living, I often face blank stares (or, worse, rapidly retreating backs) when I describe problems like the Traveling Salesman Problem.
Me: “Well, suppose the dots on this napkin represent cities, and you want to find the shortest route that visit them. How could you do it?”
Them: Quick scribble through the dots. “There! So you spend the day drawing lines through dots?”
Me: “No, no! Suppose there are 1000 cities. Then…. well, there are 1000*999*998*…*2*1 ways through all the dots, and that is more than the number of freckles on a dalmatian’s back, so I look for better ways to draw lines through dots.
And I fall into the same old trap. I try to convince people the Traveling Salesman problem is hard by saying there are a lot of solutions to look through. And that is an extremely misleading argument that I am now convinced does more harm than good.
Imagine if I had said one of the following:
- “Sorting a bunch of numbers! Hoo-wee, that’s a hard one. If I had 1000 numbers, I would have to check all orderings of the numbers to find the sorted order. That is 1000*999*998*…*2*1 orders and that is more than the hairs on a Hobbit’s toes.”
- “Maximize a linear function on n variables over m linear constraints? Well, I happen to know some theory here and know all I need to do is look at subsets of m variables and take a matrix inverse and do some checking. Unfortunately, with 1000 variables and 700 constraints, that is 1000 choose 700, which is more than the number of atoms in a brick.”
- “Find a shortest path from here to the Walmart? That’s a tough one. There are a lot of roads from here to there and I need to check all the paths to find the shortest one. That would take longer than the wait in a Comcast line!”
Of course, all of these are nonsense: having lots of possibilities may be necessary for a problem to be hard, but it is certainly not sufficient. Sorting is a problem that anyone can find a reasonable solution for. Shortest path is a bit harder, and linear programming (problem 2) is harder still. But all can be solved in time much, much less than the approaches above suggest.
So why do we use this argument for the Traveling Salesman problem? We know from complexity theory that the problem is NP-Hard, so most of us believe that there is not now a known polynomial time algorithm (there are still some who believe they have such an algorithm, but they are in the very, very tiny minority), and many of us believe that no such algorithm exists.
But that does not mean complete enumeration is necessary: it is easy to come up with approaches that go through less than the full n! solutions to the Traveling Salesman problem (see the postscript for one example). This is not surprising. Complete enumeration for Satisfiability is 2^n but there are methods known that take time proportional to something like 1.4^n [Edit: as per a comment, I meant 3-Sat]. Still exponential but not complete enumeration. And there is a big difference between 2^n and 1.00001^n (or 2^n/10^10) even if complexity theory likes to call them all “exponential”.
But the “complete enumeration” statement is even more harmful since it glosses over a much more important issue: many “hard” problems (in the complexity theory meaning) are not particularly hard (in the English sense), if you limit yourself to instances of practical interest. Due to the tremendous amount of work that has been done on the Traveling Salesman Problem, the TSP is one such problem. If you have an instance of the TSP of practical interest (i.e. it makes a difference to your life if you solve it or not, and it is really a TSP, not the result of some weird set of set of reductions from some other problem), then I bet you the Concorde program of Bill Cook and others will get you a provably optimal solution in a reasonable amount of time. In fact, I would be really interested in knowing the smallest “real” instance that Concorde cannot solve in, say, one day, on a normal laptop computer.
Being hard-to-solve in the complexity theory sense does not mean being hard-to-solve in the common language sense. And neither have much to do with the number of possible solutions that complete enumeration might go through.
As an example of this confusion, here is a paragraph from Discover on work done by Randy Olson:
Planning a vacation is a daunting task, so why not let big data take the reins?
That’s exactly what data scientist Randy Olson did. Using specialized algorithms and Google Maps, Olson computed an optimized road trip that minimizes backtracking while hitting 45 of Business Insider’s “50 Places in Europe You Need to Visit in Your Lifetime.” (Five locations were omitted simply because you can’t reach them by car.)
Mapping software has come a long way, but for this kind of challenge it’s woefully inadequate. Google Maps’ software can optimize a trip of up to 10 waypoints, and the best free route optimization software can help with 20. But when you’re looking to hit 45 or 50 landmarks, things get complicated.
According to Olson, a computer would need to evaluate 3 x 10^64 possible routes to find the best one. With current computing power, it would take 9.64 x 10^52 years to find the optimal route to hit all your desired locations — Earth would have long been consumed by the Sun before you left the house. So Olson used a clever workaround, based on the assumption that we don’t need to find the absolute best route, but one that’s pretty darn good.
Now, all this is based on an article Olson wrote months ago, and this has all be hashed over on twitter and in blogs (see here and here for example), but let me add (or repeat a few points):
- 45 points, particularly geographically based, is a tiny problem that can solved to optimality in seconds. The number of possible routes is a red herring, as per the above.
- The “based on the assumption that we don’t need to find the absolute best route, but one that’s pretty good” is not a new idea. Techniques known as “heuristics” have been around for millenia, and are an important part of the operations research toolkit.
- “Minimize backtracking” is not exactly what the problem is.
- The computer does not need to evaluate all possible routes
- With current computing power, it takes seconds (at most) to find the optimal route.
- I don’t expect the sun to consume the earth in the next minute.
- Olson’s “approach” is fine, but there are a zillion heuristics for the TSP, and it would take a very poor heuristic (maybe 2-opt by itself) not to do as well as Olson’s on this particular instance.
- Seriously, bringing in “big data”? That term really doesn’t mean anything, does it?
In Olson’s defense, let me make a few other points:
- Few of the rest of us researchers in this area are covered in Discover.
- Journalists, even science journalists, are not particularly attuned to nuance on technical issues, and Olson is not the author here.
- The instances he created are provocative and interesting.
- Anything that brings interest and attention to our field is great! Even misleading articles.
But the bottom line is that real instances of the TSP can generally be solved to optimality. If, for whatever reason, “close to optimal” is desired, there are zillions of heuristics that can do that. The world is not eagerly waiting a new TSP heuristic. Overall, the TSP is not a particularly good problem to be looking at (unless you are Bill Cook or a few other specialists): there is just too much known out there. If you do look at it, don’t look at 50 point instances: the problem is too easy to be a challenge at that size. And if you want to state that what you learn is relevant to the TSP, please read this (or at least this, for a more accessible narrative) first. There are other problems for which small instances remain challenging: can I suggest the Traveling Tournament Problem?
Finally, let’s drop the “number of solutions” argument: it makes 50 point TSPs look hard, and that is just misleading.
Postscript: an example of not needing to do complete enumeration for the Traveling Salesman Problem
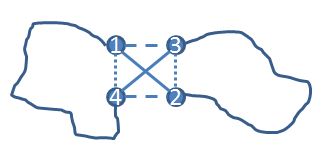
For instance, take four cities 1, 2, 3, and 4, and denote the distance matrix to be D (assumed to be symmetric, but similar arguments work for the asymmetric case). Then one of D(1,2)+D(3,4), D(1,3)+D(2,4), or D(1,4)+D(2,3) is maximum (if there are ties choose one of the maximums), say D(1,2)+D(3,4). It is easy to show that the optimal tour does not have both the edges (1,2) and (3,4), since otherwise a simple exchange would get a tour no worse. If you want to be convinced, consider the following diagram. If a tour used (1,2) and (3,4), then an alternative tour that uses either the dashed edges (1,3) and (2,4) or the dotted edges (1,4) and (2,3) would still be a tour and would be no longer than the (1,2) (3,4) tour. As drawn, the dashed edges give a shorter tour.
If you are convinced of that, then here is an algorithm that doesn’t enumerate all the tours: enumerate your tours building up city by city, but start 1, 2, 3, 4. At this point you can stop (and not move on to 1,2,3,4,5) and move on to 1,2,3,5 and so on. In doing so, we avoided enumerating (n-4)! tours. Ta da! Of course, you can do this for all foursomes of points, and don’t need to only have the foursome in the initial slots. All this can be checked quickly at each point of the enumeration tree. How many tours are we left with to go through? I don’t know: it is still exponential, but it is a heck of a lot less than n! (and is guaranteed to be less than that for any instance). Maybe even less than the time it takes for the sun to consume the earth.
Great post! This sort of talk bothers me too.
Minor quibble–we don’t know how to solve satisfiability faster than 2^n. Perhaps you’re thinking of 3SAT when you mention 1.4^n. It is a legitimate possibility that satisfiability cannot be solved faster than 2^n. In fact, this is called the strong exponential time hypothesis.