Research – Mike Trick's Operations Research Blog

Complete Enumeration Arguments Deemed Harmful…

… or “The Traveling Salesman Problem is Not That Hard”.

When I talk to people about what I do for a living, I often face blank stares (or, worse, rapidly retreating backs) when I describe problems like the Traveling Salesman Problem.

Me: “Well, suppose the dots on this napkin represent cities, and you want to find the shortest route that visit them. How could you do it?”

Them: Quick scribble through the dots. “There! So you spend the day drawing lines through dots?”

Me: “No, no! Suppose there are 1000 cities. Then…. well, there are 1000*999*998*…*2*1 ways through all the dots, and that is more than the number of freckles on a dalmatian’s back, so I look for better ways to draw lines through dots.

And I fall into the same old trap. I try to convince people the Traveling Salesman problem is hard by saying there are a lot of solutions to look through. And that is an extremely misleading argument that I am now convinced does more harm than good.

Imagine if I had said one of the following:

“Sorting a bunch of numbers! Hoo-wee, that’s a hard one. If I had 1000 numbers, I would have to check all orderings of the numbers to find the sorted order. That is 1000*999*998*…*2*1 orders and that is more than the hairs on a Hobbit’s toes.”
“Maximize a linear function on n variables over m linear constraints? Well, I happen to know some theory here and know all I need to do is look at subsets of m variables and take a matrix inverse and do some checking. Unfortunately, with 1000 variables and 700 constraints, that is 1000 choose 700, which is more than the number of atoms in a brick.”
“Find a shortest path from here to the Walmart? That’s a tough one. There are a lot of roads from here to there and I need to check all the paths to find the shortest one. That would take longer than the wait in a Comcast line!”

Of course, all of these are nonsense: having lots of possibilities may be necessary for a problem to be hard, but it is certainly not sufficient. Sorting is a problem that anyone can find a reasonable solution for. Shortest path is a bit harder, and linear programming (problem 2) is harder still. But all can be solved in time much, much less than the approaches above suggest.

So why do we use this argument for the Traveling Salesman problem? We know from complexity theory that the problem is NP-Hard, so most of us believe that there is not now a known polynomial time algorithm (there are still some who believe they have such an algorithm, but they are in the very, very tiny minority), and many of us believe that no such algorithm exists.

But that does not mean complete enumeration is necessary: it is easy to come up with approaches that go through less than the full n! solutions to the Traveling Salesman problem (see the postscript for one example). This is not surprising. Complete enumeration for Satisfiability is 2^n but there are methods known that take time proportional to something like 1.4^n [Edit: as per a comment, I meant 3-Sat]. Still exponential but not complete enumeration. And there is a big difference between 2^n and 1.00001^n (or 2^n/10^10) even if complexity theory likes to call them all “exponential”.

But the “complete enumeration” statement is even more harmful since it glosses over a much more important issue: many “hard” problems (in the complexity theory meaning) are not particularly hard (in the English sense), if you limit yourself to instances of practical interest. Due to the tremendous amount of work that has been done on the Traveling Salesman Problem, the TSP is one such problem. If you have an instance of the TSP of practical interest (i.e. it makes a difference to your life if you solve it or not, and it is really a TSP, not the result of some weird set of set of reductions from some other problem), then I bet you the Concorde program of Bill Cook and others will get you a provably optimal solution in a reasonable amount of time. In fact, I would be really interested in knowing the smallest “real” instance that Concorde cannot solve in, say, one day, on a normal laptop computer.

Being hard-to-solve in the complexity theory sense does not mean being hard-to-solve in the common language sense. And neither have much to do with the number of possible solutions that complete enumeration might go through.

As an example of this confusion, here is a paragraph from Discover on work done by Randy Olson:

Planning a vacation is a daunting task, so why not let big data take the reins?

That’s exactly what data scientist Randy Olson did. Using specialized algorithms and Google Maps, Olson computed an optimized road trip that minimizes backtracking while hitting 45 of Business Insider’s “50 Places in Europe You Need to Visit in Your Lifetime.” (Five locations were omitted simply because you can’t reach them by car.)

Mapping software has come a long way, but for this kind of challenge it’s woefully inadequate. Google Maps’ software can optimize a trip of up to 10 waypoints, and the best free route optimization software can help with 20. But when you’re looking to hit 45 or 50 landmarks, things get complicated.

According to Olson, a computer would need to evaluate 3 x 10^64 possible routes to find the best one. With current computing power, it would take 9.64 x 10^52 years to find the optimal route to hit all your desired locations — Earth would have long been consumed by the Sun before you left the house. So Olson used a clever workaround, based on the assumption that we don’t need to find the absolute best route, but one that’s pretty darn good.

Now, all this is based on an article Olson wrote months ago, and this has all be hashed over on twitter and in blogs (see here and here for example), but let me add (or repeat a few points):

45 points, particularly geographically based, is a tiny problem that can solved to optimality in seconds. The number of possible routes is a red herring, as per the above.
The “based on the assumption that we don’t need to find the absolute best route, but one that’s pretty good” is not a new idea. Techniques known as “heuristics” have been around for millenia, and are an important part of the operations research toolkit.
“Minimize backtracking” is not exactly what the problem is.
The computer does not need to evaluate all possible routes
With current computing power, it takes seconds (at most) to find the optimal route.
I don’t expect the sun to consume the earth in the next minute.
Olson’s “approach” is fine, but there are a zillion heuristics for the TSP, and it would take a very poor heuristic (maybe 2-opt by itself) not to do as well as Olson’s on this particular instance.
Seriously, bringing in “big data”? That term really doesn’t mean anything, does it?

In Olson’s defense, let me make a few other points:

Few of the rest of us researchers in this area are covered in Discover.
Journalists, even science journalists, are not particularly attuned to nuance on technical issues, and Olson is not the author here.
The instances he created are provocative and interesting.
Anything that brings interest and attention to our field is great! Even misleading articles.

But the bottom line is that real instances of the TSP can generally be solved to optimality. If, for whatever reason, “close to optimal” is desired, there are zillions of heuristics that can do that. The world is not eagerly waiting a new TSP heuristic. Overall, the TSP is not a particularly good problem to be looking at (unless you are Bill Cook or a few other specialists): there is just too much known out there. If you do look at it, don’t look at 50 point instances: the problem is too easy to be a challenge at that size. And if you want to state that what you learn is relevant to the TSP, please read this (or at least this, for a more accessible narrative) first. There are other problems for which small instances remain challenging: can I suggest the Traveling Tournament Problem?

Finally, let’s drop the “number of solutions” argument: it makes 50 point TSPs look hard, and that is just misleading.

Postscript: an example of not needing to do complete enumeration for the Traveling Salesman Problem

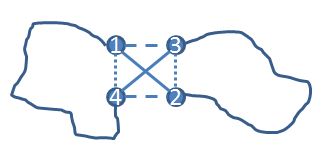
For instance, take four cities 1, 2, 3, and 4, and denote the distance matrix to be D (assumed to be symmetric, but similar arguments work for the asymmetric case). Then one of D(1,2)+D(3,4), D(1,3)+D(2,4), or D(1,4)+D(2,3) is maximum (if there are ties choose one of the maximums), say D(1,2)+D(3,4). It is easy to show that the optimal tour does not have both the edges (1,2) and (3,4), since otherwise a simple exchange would get a tour no worse. If you want to be convinced, consider the following diagram. If a tour used (1,2) and (3,4), then an alternative tour that uses either the dashed edges (1,3) and (2,4) or the dotted edges (1,4) and (2,3) would still be a tour and would be no longer than the (1,2) (3,4) tour. As drawn, the dashed edges give a shorter tour.

If you are convinced of that, then here is an algorithm that doesn’t enumerate all the tours: enumerate your tours building up city by city, but start 1, 2, 3, 4. At this point you can stop (and not move on to 1,2,3,4,5) and move on to 1,2,3,5 and so on. In doing so, we avoided enumerating (n-4)! tours. Ta da! Of course, you can do this for all foursomes of points, and don’t need to only have the foursome in the initial slots. All this can be checked quickly at each point of the enumeration tree. How many tours are we left with to go through? I don’t know: it is still exponential, but it is a heck of a lot less than n! (and is guaranteed to be less than that for any instance). Maybe even less than the time it takes for the sun to consume the earth.

Quantum computing and operations research

Quantum computing is one of those weird ideas out there that will either change the world or go the way of cold fusion, so I periodically think I need to learn more about the area. I am by no means an expert (or even knowledgeable) in the area. My expertise comes from reading Scott Aaronson’s blog, which makes me as knowledgeable as about about a million other people out there. Seeing a series of papers showing how quantum computing can factor numbers is interesting, until you realize that the number involved are still well in the range of what my eight year old can do in his head. There are a lot better ways to spend my research time.

So, when a paper comes out involving using quantum computers to solve NP-hard problems (for a paper just presented at the ACM Conference on Computing Frontiers), I didn’t exactly leap at the opportunity to read it. That was until I saw the senior author: Cathy McGoech (the other coauthor is doctoral student Cong Wang). Cathy is the real deal. I have met her a few times, but I don’t know her well personally. But her research has had a big effect on me. Cathy, together with David Johnson (of Johnson and Garey fame) began the DIMACS Challenges twenty years ago. The goal in these challenges is to look at real-life algorithmic performance. The two of them ran the first Challenge (on Network Flows and Matchings); I ran the second Challenge, on cliques, coloring, and satisfiability. Cathy was extremely influential in how I thought about the Challenge. In particular, how can one distinguish between “fast coding” and “fast algorithms”? And what do interesting computational questions look like? I certainly never got to her level of sophistication when it comes to experimental design and evaluation, but her work made me better.

My research has moved off in my dillettante way to other things; Cathy has continued to work very hard to put experimental algorithmics on a solid footing. She even has a new book out on the topic (which I just ordered).

All this means: if Cathy is saying something about a computational evaluation, it is going to be worth listening to.

Short synopsis: Cathy and her coauthor got access to a D-Wave Two platform, heuristically solved a number of instances of three NP-Hard problems (Quadratic Unconstrained Binary Optimization, Weighted Maximum Two-Satisfiability, and Quadratic Assignment), and generally performed much faster than methods such as CPLEX.

The D-Wave platform has caused some controversy, since it is unclear what exactly happens in the system. The “holy grail”, as I understand it (it is not Aaronson’s fault if I get this wrong!) is quantum entanglement. This sort of “action at a distance” is key to much of the theory behind quantum computing. Does D-Wave get this? The paper covers this:

Finally there has been some debate as to whether D-Wave chips form a ‘truly’ quantum system; this has been demonstrated for smaller (8 and 16 qubit) systems … but
not, as yet, for the full hardware graph. Boixo et al.
report that the hardware demonstrates quantum tunneling
(which would be inconsistent with classical annealing), and
find some evidence of qubit entanglement. A recent review
article in Science [ Science, 13 May 2011] concludes that the hardware is at least a little quantum mechanical.

I suppose the researchers ended up at least a little tenured for this work.

But how does it work? Generally, pretty well:

In all three experiments the V5 hardware or its hybrid counterpart Blackbox found
solutions that tied or bettered the best solutions found by
software solvers. Performance was especially impressive on
instances that can be solved directly in hardware. On the
largest problem sizes tested, the V5 chip found optimal so-
lutions in less than half a second, while the best software
solver, CPLEX, needed 30 minutes to find all optimal solutions.

We have also carried out some tests to compare V6 to
the software solvers; very preliminary results suggest that
on QUBO instances with n = 503, the hardware can find
optimal solutions around 10,000 times faster than CPLEX.

Pretty impressive sounding, and certainly something worth paying attention to.

But still, it is important to understand some key aspects of this work:

1) The solutions found are “just” heuristic solutions. There is no proof of optimality, nor can there be with the setup being used. In essence, we are getting a very fast population search with what looks like simulated annealing.

2) The comparator is primarily CPLEX, a code designed for finding and proving optimal solutions. I have refereed 3 papers in the last month alone that give heuristics that are orders of magnitude faster than CPLEX in finding good solutions. Of course, CPLEX is generally infinitely faster in proving optimality (since it wins whenever it proves optimality). Beating CPLEX by orders of magnitude on some problems in finding good solutions (particularly with short times) does not require fancy computing.

3) The problems chosen are not exactly in CPLEX’s sweet spot. Consider maximum weighted 2-SAT, where the goal is to maximize the weight of satisfied clauses in a satisfiability problem, where each clause has exactly two variables. The natural linear relaxation of this problem results in a solution with all variables taking on value .5, which gives no guidance to the branch-and-bound search. Now CPLEX has a lot of stuff going on to get around these problems, but there are certainly NP-Hard problems for which CPLEX has better relaxations, and hence better performance. And if you take any sort of problem and add complicating constraints (say, max weighted 2-sat with restrictions on the number of TRUE values in various subsets of variables), I’ll put my money on CPLEX.

4) The D-Wave system is still a bit pricey: at about $10,000,000, there are cheaper ways to get the sort of speedup that McGeoch and Wang found.

Cathy understands the comparator issue:

It would of course be interesting to see if highly tuned
implementations of, say, tabu search or simulated annealing
could compete with Blackbox or even QA on QUBO prob-
lems; some preliminary work on this question is underway.

Despite these qualms, Cathy has gotten me interested.

Google too, by the looks of it.

Be sure to check out Scott Aaronson’s take on this, as he resumes his role as “Chief D-Wave Skeptic”.

Summer Internship at IBM Research, AI for Optimization Group

Just saw this announcement of a summer internship

A summer internship position is available for 2013 in the “AI for Optimization” group within the Business Analytics and Mathematical Sciences department at IBM Watson Research Center, Yorktown Heights, New York. The internship will last for about 3 months and will be scheduled between March and October, 2013.

Candidates should be exceptional Masters or PhD students in Computer Science and related areas, and not have already received their PhD by the internship start date. The successful candidate is expected to have strong interest and some experience in one or more of the following:

+ Developing Novel Technologies based on AI and OR to advance the state of the art in combinatorial optimization (e.g., Heuristic Search, Mixed Integer Programming (MIP), Linear Programming (LP), Satisfiability (SAT))

+ Robust Parallelization of search-based algorithms (e.g., using parallel Branch&Bound; information exchange) exploiting novel computing architectures such as BlueGene, multi-core end-user machines, large compute clusters, and the Cloud

+ Advancing Simulation-Based Optimization approaches to solve real-world problems and/or to improve optimization methods themselves by, e.g., employing techniques from Machine Learning, Local Search, and Genetic Algorithms for automated algorithm selection and parameter tuning

+ Applications of Optimization to Analytics, Production Modeling, Sustainability, Systems, and Databases

Interested candidates should send their CV as well as names and contact information of at least two references to all of the following:

Ashish Sabharwal [ashish.sabharwal@us.ibm.com]
Horst Samulowitz [samulowitz@us.ibm.com]
Meinolf Sellmann [meinolf@us.ibm.com]

I wish I didn’t already have my PhD!

Easy and Hard Problems in Practice

David Eppstein of the blog 0xde has a list of his top 10 preprints in algorithms in 2012. One particularly caught my eye:

Clustering is difficult only when it does not matter, Amit Daniely, Nati Linial, and Michael Saks, arXiv:1205.4891. […] this represents a move from worst-case complexity towards something more instance-based. The main idea here is that the only hard instances for clustering problems (under traditional worst-case algorithms) are ones in which the input is not actually clustered very well. Their definition of a “good clustering” seems very sensitive to outliers or noisy data, but perhaps that can be a subject for future work.

This paper really hit home for me. I have taught data mining quite often to the MBAs at the Tepper School and clustering is one topic I cover (in fact, research on clustering got me interested in data mining in the first place). I generally cover k-means clustering (easy to explain, nice graphics, pretty intuitive), and note that the clustering you end up with depends on the randomly-generated starting centroids. This is somewhat bothersome until you play with the method for a while and see that, generally, k-means works pretty well and pretty consistently as long as the data actually has a good clustering (with the correct number of clusters). It is only when the data doesn’t cluster well that k-means depends strongly on the starting clusters. This makes the starting centroid issue much less important: if it is important, then you shouldn’t be doing clustering anyway.

There are other operations research algorithms where I don’t think similar results occur. In my work in practice with integer programming, most practical integer programs turn out to be difficult to solve. There are at least a couple of reasons for this (in addition to the explanation “Trick is bad at solving integer programs”). Most obviously, easy problems typically don’t get the full “operations research” treatment. If the solution to a problem is obvious, it is less likely to require more advanced analytics (like integer programming and similar).

More subtly, there is a problem-solving dynamic at work. If an instance is easy to solve, then the decision maker will do something to make it harder. Constraints will be tightened (“What if we require at least 3 weeks between consecutive visits instead of just two?”) or details will be added (“Can we add the lunch breaks?”) until the result becomes a challenge to solve. I have not yet had a real-world situation where we exhausted the possibilities to add details to models or to further explore the possible sets of constraints. Eventually, we get to something that we can’t solve in a reasonable amount of time and we back up to something we can (just) solve. So we live on the boundary of what can be done. Fortunately, that boundary gets pushed back every year.

I am sure there is a lot of practical work in operations research that does not have this property. But I don’t think I will wake up one morning to see a preprint: “Integer programming is difficult only when it doesn’t matter”.

Referees considered harmful

When doing empirical work, researchers often mess up either in the design of the experiment or in the analysis of data. In operations research, much of our “empirical work” is in computational testing of algorithms. Is algorithm A faster than algorithm B? “It depends” is generally the only honest answer. It depends on the instance selection, it depends on the computing environment, it depends on the settings, etc. etc. If we are careful enough, we can say things that are (within the limits of the disclaimers) true. But even a a careful experiment can fall prey to issues. For instance, throwing away “easy” instances can bias the results against whatever algorithm is used to determine easiness. And don’t get me started on empirical approaches that test dozens of possibilities and miraculously find something “statistically significant”, to be duly marked with an asterisk in the table of results. It is very difficult to truly do trustworthy empirical work. And it is even harder to do such work when researchers cheat or reviewers don’t do their job.

For some fields, these issues are even more critical. Operations research generally has some theoretical grounding: we know about polytopes and complexity, and so on, and can prove theorems that help guide our empirical work. In fields like Social Psychology (the study of people in their interactions with others), practically all that is known is due to the results of experiments. The fundamental structure in this field is a mental state, something that can only be imprecisely observed.

Social psychology is in a bit of a crisis. In a very real sense, the field no longer knows what is true. Some of that crisis is due to academic malfeasance, particularly that of an influential researcher Diederik Stapel. Stapel has been found inventing data for dozens of papers, as described by a “Science Insider” column.

Due to data fraud by Stapel and others, the field has to reexamine much of what it thought was true. Are meat eaters more selfish than vegetarians? We thought so for a while, but now we don’t know. A Dutch report on this goes into great detail on this affair.

But overt fraud is not the only issue, as outlined in the report. I was particularly struck by the role paper reviewers played in this deceit:

It is almost inconceivable that co-authors who analysed the data intensively, or reviewers of the international “leading journals”, who are deemed to be experts in their field, could have failed to see that a reported experiment would have been almost infeasible in practice, did not notice the reporting of impossible statistical results, … and did not spot values identical to many decimal places in entire series of means in the published tables. Virtually nothing of all the impossibilities, peculiarities and sloppiness mentioned in this report was observed by all these local, national and international members of the field, and no suspicion of fraud whatsoever arose.

And the role of reviewers goes beyond that of negligence:

Reviewers have also requested that not all executed analyses be reported, for example by simply leaving unmentioned any conditions for which no effects had been found, although effects were originally expected. Sometimes reviewers insisted on retrospective pilot studies, which were then reported as having been performed in advance. In this way the experiments and choices of items are justified with the benefit of hindsight.

Not infrequently reviews were strongly in favour of telling an interesting, elegant, concise and compelling story, possibly at the expense of the necessary scientific diligence.

I think it is safe to say that these issues are not unique to social psychology. I think that I too have, as a reviewer, pushed toward telling an interesting story, although I hope not at the expense of scientific diligence. And perhaps I could have worked harder to replicate some results during the reviewing process.

I don’t think we in operations research are in crisis over empirical issues. I am pretty confident that CPLEX 12.4 is faster than CPLEX 4.0 for practically any instance you can throw at it. And some journals, like Mathematical Programming Computation have attempted to seriously address these issues. But I am also pretty sure that some things I think are true are not true, either due to fraud by the author or negligence by reviewers.

One important role of a reviewer is to be on the lookout for malfeasance or bias and to avoid allowing (or, worse, forcing) authors to present data in an untruthful way. And I think many of us are not doing a great job in this regard. I would hate to have to rethink the foundations of my field due to these issues.

The cutting plane method for matching is polynomial

Michael Mitzenmacher is a computer scientist at Harvard with a blog My Biased Coin. As you might expect from the title, Michael works in the area of randomized algorithms, and even has a book on the subject. His blog is an extremely useful guide to the what is happening in algorithms in CS (and what is happening in CS at Harvard, which is also quite interesting). He often provides a summary of talks given at the big theory conferences (FOCS/STOC/etc.). He just posted on this year’s FOCS (here and here).

There was one talk that caught my eye, summarized by a doctoral student:

[Editor: Fourth-year grad student Justin Thaler of Harvard contributes a summary of two unrelated talks.]

Paper Title: The Cutting Plane Method is Polynomial for Perfect Matchings.

Harvard’s own Karthekeyan Chandrasekaran talked about joint work with Laszlo A. Vegh and Santosh S. Vempala on cutting plane algorithms for matching problems. The cutting plane method is a popular algorithm for solving integer programs (IPs), used in commercial solvers. It works by starting with an LP relaxation of the given IP to obtain basic optimal solution x_0, and then iteratively adding constraints that are valid for integer solutions but violated by the basic optimum. It continues until the basic optimum is integral. The goal of this paper is to take a step toward explaining the practical efficiency of cutting plane methods, by giving an efficient cutting-plane algorithm for min-cost perfect matching (MWPM) –MWPM is known to be in P, but it was open (apparently for 30 years) whether there was a polynomial-time cutting-plane algorithm for this problem.

A brief summary of how they achieve this is as follows. They start with a natural, well-known LP relaxation of the MWPM problem, called the bipartite relaxation. This relaxation has the nice property that all basic optima x are half-integral, and the support of x is a disjoint union of edges and odd cycles. This makes it easy to find cuts (the cuts correspond to what are called blossom inequalities, see the paper for details). A major challenge, though, is that naively adding cuts will not preserve the half-integrality of intermediate LPs, so at each iteration they throw away some of the old cuts that were added earlier in the execution. They need to take considerable care in choosing which cuts to keep in order to guarantee half-integrality of intermediate LPs (and to ensure that their algorithm makes progress at a sufficiently high rate).

This is pretty amazing. First, it is wonderful that they were able to prove polynomiality. It had bothered me that it seemed you might need an exponential number of cuts, even for something like matching. I had looked at this 25 years ago when doing my doctorate, but didn’t have any particularly insightful ideas.

But the really amazing thing is that they were able to arrange their algorithm so they never had to work with anything worse than half-integral solutions. This is astounding! A bane of cutting plane approaches is the weird fractions that keep popping up, leading to numerical stability problems. Here, they were able to keep things well under control. And, by keeping to half-integral, maybe some old ideas I had about using generalized networks (networks with multipliers) might come back into play. The approach certainly avoids the need for Gomory-Hu cut tree approaches to finding violated inequalities: violated inequalities come straight out of connected components. This also harkens back to my dissertation where I had treated matching as a generalized network with side constraints.

So I checked out the paper that underlies the talk at arXiv, thinking I might try to implement some things this week and see how it works (CS theory people rarely implement: you could make an entire career out of simply implementing what CS people suggest). On the plus side, they reference my dissertation, so at least I am in the right ballpark. On the down side: it is looking a bit complicated! Looks like I will have to reel in one of the bright doctoral students around to plow through this with me.

And I wonder what else this might be used for?

Fischetti Speeds Up Optimization with Randomness

I just got back from a very nice workshop on “Matheuristics” held outside of Rio de Janeiro, Brazil. Matheuristics is the combination of optimization and heuristics. For instance, I talked about large scale local search for sports scheduling problems (among other things). In this approach, portions of a sports schedule are fixed, and you optimize over the rest using integer programming. This has aspects of both metaheuristics (large scale local search) and optimization (integer programming).

I greatly enjoyed the workshop and thank Celso Ribeiro for organizing it and inviting me. It was a small workshop, with perhaps 40 participants, with a single track of papers. For the first time in years I attended every talk at a conference! Try doing that at INFORMS!

My favorite talk was given by Matteo Fischetti of the University of Padova. The talk, entitled “Erraticism in tree search” was a real eye opener in terms of my understanding of how branch-and-bound on integer programs performs in practice. I’m going to paraphrase some of the key points of the talk. None of the numbers in the following are exactly what Matteo presented, but this is close enough to get the idea across.

Here’s the setup: Matteo claims to have a new cut for general mixed integer programs. It is parameterized, so he can actually create 10 different versions of that cut. He downloaded the MIPLIB 2010 benchmarks and some other benchmarks he found, ran default CPLEX on them, and limited his test to hard, but not insolvable instances (tossing out all instances solved by default CPLEX in under 100 seconds or requiring more than 1000 seconds). This left a test bed of 38 instances.

When Matteo solved the testbed using each of the ten cuts (separately), he found something amazing: a single cut often greatly decreased computation time. The (geometric) average decreases over the testbed relative to default CPLEX for the ten different parameterizations were:

Parametrization		1	2	3	4	5	6	7	8	9	10
Decrease		12%	14%	25%	4%	-0.50%	32%	15%	12%	6%	33%

Wow! These cuts are great! Cut 5 had a bit of an increase in time, but it turned out that cut was kind of a dummy. Cut 5 took a random permutation of the non-negative integer variables and added a constraint Σ xi ≥ -1. This constraint clearly doesn’t do anything: CPLEX throws it away during preprocessing.

But look at Cut 10. It decreased computation time by 33%. It is amazing! Cut 10 took a random permutation of the non-negative integer variables and added a constraint Σ xi ≥ -1. And that seems to work really well!

Hold on…. What’s going on here? In fact, each of the cuts is simply a random permutation of the variables and a redundant constraint. How can that have any effect?

CPLEX (as with Gurobi or any other solver) has a certain “randomness” in its operation. This is not random in the sense that the final answers are not optimal, but rather the exact operation of the algorithm may depend on things like the ordering of the variables. So, for instance, if a solution to a linear program has multiple optimal solutions, the exact solution reported can depend on which variable is first in the internal ordering of variables. And, of course, the exact solution reported can then affect the branch and bound tree (since different variables might have fractional values).

If you change the internal ordering of the variables, you can change the operation of the branch and bound algorithm. Adding the redundant cut changed the internal ordering of the variables, so the timing results could vary. Not every instance has this aspect. Some have relatively consistent computation time independent of the ordering. But some instances vary a lot based on the ordering.

This is insight 1: branch and bound timings may vary a lot due just to the random choices of the algorithm.

If your computation time is too long, try permuting the variables. If you see lots of variation in computing time, perhaps it it is worth running multiple instances in parallel with different variable orderings (or internal random number seeds) in the hopes that one instance will solve much faster than the others.

This makes me wonder how many past papers showing that an approach is useful are simply showing different (good) random draws from the search tree? And how many good ideas have been discarded due to “bad luck” from the random number generator?

But this still leaves a puzzle: almost every random ordering is better than default CPLEX. Does this mean that you should at least randomly generate an variable ordering? One gentleman at the conference, vibrating with excitement, thought he had the justification for this:

Since most of these instances come from real problems, perhaps there is something about the way people formulate problems that leads to problems with the solution code. As I code, I would normally generate all of one type of variable (say, the “x” variables), then the “y” variables, then the “z” variables. This must be messing up CPLEX. What a great insight!

That hyperventilating gentleman was me. And Matteo quickly and firmly showed that I was wrong. How could almost all of the orderings do better than default CPLEX? Look back, the hint is there…..

How did we get our instances? Let me quote myself:

He downloaded the MIP2010 benchmarks and some other benchmarks he found, ran default CPLEX on them, and limited his test to hard, but not insolvable instances (tossing out all instances solved by default CPLEX in under 100 seconds or requiring more than 1000 seconds).

In doing this, he biased the sample! Anything default CPLEX did well on (under 100 seconds), we threw out! So the sample was made up of things that default CPLEX did not do well on. It is no wonder that “Cut 1” had an advantage. If we had run all the instances on “Cut 1” and threw out anything it did well on, it would turn out the default CPLEX would do better than “Cut 1”. If you toss out instances that an algorithm works well on, don’t be surprised if it does poorly on the rest.

So this is insight 2: if you want to compare algorithms A and B, make sure the definition of the testbed does not depend on which gets label A and which gets label B.

I can’t tell you the number of times I have read computational papers that make the bias mistake. And I rarely noticed it. I will now!

Of course, Matteo doesn’t make mistakes like this in his work: this presentation was an extremely effective way of showing how easy it is to make this error.

I cannot do full justice to Matteo’s talk: there were many more insights and surprises. The associated paper (with Michele Monaci) is here. And if you get a chance to see him give the talk, do so!

After that talk, I will never look at computation in integer programming the same way again. That presentation alone was worth the flight to Brazil!

Added 9/26: Matteo has kindly provided his slides, which are available here.

A Love Letter to the Traveling Salesman Problem

Bill Cook of Georgia Tech has a new book out on the Traveling Salesman Problem entitled “In Pursuit of the Traveling Salesman” from Princeton University Press (or from Amazon or B&N). Unlike his previous book (with David Applegate, Bob Bixby and Vašek Chvátal), this book is aimed at a general audience. Bill takes his readers down a beautiful path covering the history, applications, and algorithms associated with the TSP. It is a fascinating story, and one that shows a researcher who truly loves his research area. You would think such a love was common among researchers, but I have seen many researchers who seem bored by, or positively hate, their research areas. Bill is obviously enraptured by the TSP.

The Traveling Salesman Problem is remarkable easy to state: given a set of points with distances between them, find the shortest tour through all the points. For example, as Bill wrote about recently, given 99 towns in Iowa to visit and the road distances between every pair, what is the quickest way to see all the cities, returning to your starting position?

Despite its simple statement, the problem of finding good or optimal tours has generated thousands of research papers. The TSP is the standard testbed for discrete optimization: practically every possible approach to optimization can be tried out on the TSP. So research on the TSP has had a tremendous effect on approaches for all sorts of other optimization problems. Bill covers every aspect of this research corpus.

Perhaps the most interesting part about this book is that Bill pulls no punches when it comes to presenting work. Most of us would be tempted to go only so deep into an area and then start hand-waving believing “well, no one would understand this area anyway”. Here is how Bill begins a description of finding comb inequalities, a type of constraint necessary to determine the TSP polytope:

Subtour-elimination constraints? No problem. Comb inequalities? Not so good.
At the moment there is no known polynomial-time algorithm that is guaranteed to
spot a violated comb inequality if one exists. The comb-separation problem is also
not known to be in the NP-complete complexity class, so its status is wide open.
A great need coupled with inconclusive results translates into an important research
problem.

This is not to say that combs are currently skipped over in computations. By
hook or by crook computer codes must generate combs to push LP bounds after
subtour-elimination constraints fail. This is accomplished by hit-or-miss strategies
for growing handles, shrinking teeth, splicing sets, and a host of other operations.

If I tried to write this book, I don’t think I would have even got to comb inequalities, let alone continued to the nice description Bill provides of comb-finding heuristics. This level of discussion requires some concentration when reading but the book is accessible to a wide audience. This is an ideal book to get a college student or a smart high school student interested in operations research and combinatorial optimization.

This is a highly personal look at the TSP. Bill tells you his favorite heuristic (farthest insertion), his favorite exotic computing model (time traveling solver: take as long as you like to solve but then go back in time to report the solution), and much more.

Chapters have interesting lead quotes (the book begins with Listen, mate, I’ve traveled every road in this here land. from Geoff Mack in the song “I’ve Been Everywhere”), and the illustrations throughout are fantastic. I also love the way that Bill includes pictures of practically everyone who has done research in this area. Putting faces to the names is a wonderful way to personalize the research.

Through this book, you’ll learn all about the Traveling Salesman Problem and, more broadly, about the different research directions in combinatorial optimization. And you’ll also see why top-notch researchers like Bill Cook find the TSP endlessly fascinating. And you might just want to be a researcher like Bill.

I guess a bit of a disclaimer is needed here: Bill has included a very nice mention of this blog in the book (thanks Bill!) with a picture of me, and his publisher sent me an advance copy of the book. I failed miserably in getting a nice quote in on time, but that is due to my own failings. I really love the book!

16 Clue Sudokus

I am sure everyone has seen Sudoku puzzles: it was quite a fad a few years ago. The puzzle begins with an 9×9 grid, partially filled with numbers from 1 to 9 (the “givens”). The goal is to complete the grid so that that every row, column, and the nine 3×3 subgrids in the corners and center all contain the numbers 1 through 9 with no missing and none repeated. There was a time in my life where I loved Sudoku puzzles. I had to give them up when I started to dream solely in Sudoku.

The puzzles can be difficult or easy depending on straightforward it is to deduce missing values. A grid with many givens tends to be very easy, since there are few choices for missing values (though there can be hard problems with many givens and easy ones with few). If too few values are filled in, however, the solution may not be unique, and it is a fundamental precept of puzzle-creators that the solution must be unique. So, how many givens are needed to ensure uniqueness? It has been known for a long time that there exist problems with 17 givens that lead to unique solutions.

Gary McGuire, Bastian Tugemann, Gilles Civario of University College Dublin proved this result is the best possible: there is no problem with 16 givens with a unique solution. They do this in a very interesting way: they did an exhaustive search. Given the number of possible solutions, it is surprising that exhaustive search works, but they were clever in organizing the search, and had access to a ridiculous amount of computational power. This combination let them run through all the choices. They didn’t find a 16, therefore there is not a sixteen!

Fascinating work, and a sign of how fast computing can change how we look at research problems. Technology Review has an article on this; the technical report is at arXiv.

Super Exciting News on Super Polynomiality of LP Formulations of the TSP Polytope

Years ago, I spent a very pleasant couple of weeks in a group debunking a claimed linear programming formulation of the Traveling Salesman Problem. I wrote on this before, and bewailed the fact that I was not smart enough to figure out there was a general theorem there: Yannakakis showed that no symmetric linear programming formulation of polynomial size can formulate the TSP. The “symmetric” part of the theorem was always bothersome since it seemed an unnecessary addition. You can make a symmetric formulation “unsymmetric” by doing something goofy in adding a useless variable or similar, but the fundamental result still holds. Can asymmetry work on a fundamental level? I worked on trying to remove the symmetric assumption, but had no success. That’s not surprising since Yannakakis clearly would have not included the requirement if it was easy to remove. Yannakakis is smarter than Trick. Therefore Trick cannot remove the requirement. Q.E.D. But I still tried for a while.

Fortunately, research moves on, and people learn more and more, and finally enough gets proved that smart people can figure out how to move forward. It appears that the symmetric requirement can be removed. Sebastian Pokutta, and his coauthors Samuel Fiorini, Serge Massar, Hans Raj Tiwary, and Ronal de Wolf have a paper that proves that any linear programming formulation (symmetric or not) of the TSP is ~~exponentially sized~~ super polynomial. Sebastian’s blog post has a very nice description of some recent history (including the astonishing result that sometimes the symmetry requirement does matter) and gives pointers to both the paper and to some slides. I have not had time to go through things thoroughly (or at all, really) but the paper seems a trove of interesting results. I feel like starting a Ph.D. seminar next week to study it!

Between Bill Cook’s soon-to-be-released TSP book and this news, 2012 is shaping up to the be the year of the Traveling Salesman Problem!