During the last winter Olympics, I had what I thought was a pretty good idea. There are many ways to rank countries during the Olympics: you can rank them by total number of medals, or you can rank them by number of gold medals, or by some point scheme (5 for gold, 3 for silver, 1 for bronze) and so on. Point schemes seem to make sense, but then people argue about points. Is a gold worth 5 bronzes or 4? Is 2 silvers more than, less than, or the same as a gold?
So my idea was to rank countries by the fraction of reasonable weights that result in them having the highest point count. Not every point scheme is reasonable: only a bronze lover (pyropusaphile?) would score bronze higher than gold. So we need gold >= silver >= bronze. And it seems unreasonable to have a negative weight on a medal. Finally, the weights can be scaled so that the total weight is one.
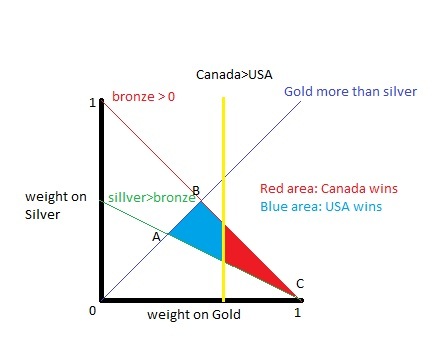 In the Winter 2010 Olympics, Canada was edged out by the United States in the Trick Medal Championship (TMC) by a narrow margin. Canada had 14 gold, 7 silver, and 5 bronze; the US went 9, 15, 13. If you put enough weight on gold, then Canada wins. But only 45.25% of the reasonable weights put enough weight on Gold for Canada to win; the US wins for the remaining 54.75% of the weights.
In the Winter 2010 Olympics, Canada was edged out by the United States in the Trick Medal Championship (TMC) by a narrow margin. Canada had 14 gold, 7 silver, and 5 bronze; the US went 9, 15, 13. If you put enough weight on gold, then Canada wins. But only 45.25% of the reasonable weights put enough weight on Gold for Canada to win; the US wins for the remaining 54.75% of the weights.
The summer Olympics are now over, with the final medal count being:
US: 46,29,29
China: 38,27,22
Russia: 24,25,33
Great Britain: 29, 17,19
with no other country winning at least 20 medals of a single type.
So the coveted TMC Award goes to …. the United States in a rout! In fact, the US wins for every reasonable weighting. Russia could win with a lot of weight on bronze medals, but not if the weight on gold and silver is at least that of bronze.
A necessary and sufficient condition to win for any reasonable weight is to have
- more gold than anyone else,
- more gold+silver than anyone else, and
- more gold+silver+bronze than anyone else.
Equality in any of these can lead to weights where the country ties for the win.
Here, the US meets that condition. Of course, it helps that there are a zillion medals in swimming (where the US does well) and only one in, say, team handball (described here as water polo without the water, which is only marginally informative). But a win is a win: if any representative of the US Olympic teams would like to drop by my office, I will be glad to give them the TMC trophy (which I will be recycling from my stash of high-school curling trophies I have dragged around the world).
P.S. The Wall Street Journal Numbers Guy has a similar discussion though, sadly, it does not include the above approach.
Go USA!!!! Nice Article and different perspective.
Rick
[non Operations Research URL deleted]
Why would you weight these, rather than leaving them (properly) as multiple objectives? That is:more gold than everybody else, more silver than everybody else, and more bronze than everybody else?
Weighted schemes for collapsing multiple objectives are always premature, especially in exploratory work.
Reverse engineering on multi-criteria weighting is a funny game.
If I were from Great Britain, I would claim to divide the score by population size. In the case of China, I would argue to divide by absolute GDP. As for Russia, well, what about multiplying by average temperature? Summer games often require outdoor practice, which is not always possible there.
@Bill: ignoring the chosen additive form with weights, I think a reasonable axiom for a multi-objective scoring system in this context would be that winning a bronze should never be preferred to winning a silver, and winning a silver should never be preferred to winning a gold. Given this axiom, I believe the necessary and sufficient condition given is still correct.
If your point is that non-additive scoring functions should be considered, that’s certainly valid, but makes the space of possible functions much less transparent.
Medal tables are not compatible with the Olympic “concept” (~ spirit, idea):
> “The Olympic Games are competitions between athletes in individual or team events and not between countries” “The IOC […] shall not draw up any global ranking per country.” [http://en.wikipedia.org/wiki/Olympic_medal_table#Background]
Where the IOC leaves a void, I leap to fill it!
@Thiago: I’m sure China would be more excited to divide the medal count by per capita GDP.