It is Labor Day weekend here in the US, so, in addition to the mandatory grilling and bicycling with Alexander, I have some time to laze about on the porch reading books (and drinking beer, which is also legally required in my jurisdiction). I have been reading Numbers Rule by George Szpiro. This is a fascinating book on the history of thought about voting rules, starting back with Plato and continuing with Pliny the Younger, Llull, Cusanus, Borda, Condorcet, Laplace, Dodgson, and ending with the impossibility results of Arrow, Gibbard, and Satterthwaite. Interleaved are a few chapters on the problem of allocating seats in a parliament.
I have done work in this area (and Bartholdi, Tovey and Trick even make an appearance on page 115) but I don’t consider myself a specialist. Even specialists, however, might learn something on the history of the field from this book. The Llull-Casanus period (roughly 1200 A.D. to 1450 A.D.) in particular was new to me. This pre-Renaissance period was not one that generally generated a lot of deep insights into non-religious issues (in the Western world), but voting was one area that was of great interest to the ecclesiasticals, most notably in the election of the Pope, but also in electing people for lesser positions such as abbot.
Voting seems to be an easy problem: we do it all the time. “How many people want A? How many people want B? OK, A wins” is certainly used in our three-person household. But voting is much harder when there are more than two possible outcomes. With A, B, and C as possibilities, having each elector vote for one and then taking the one with the most votes (plurality elections) leads to all sorts of bad outcomes. For instance, it is arguable that having Nader in the 2000 election with Bush and Gore (in the U.S. Presidential election) led to Bush winning while without Nader, Gore would have won. This is an example of violation of “Independence of Irrelevant Alternatives”: shouldn’t an election result be consistent whether or not a third (or fourth or fifth) candidate enters? In other words, if A beats B when only the two run, if C also runs then it should be that either C wins or A continues to win. Stands to reason! But plurality voting is terrible with respect to this condition, so “splitting the opposition” is a standard way to strategically manipulate such an election.
The book makes it clear that issues of fairness in elections with more than two candidates go back to Greek times. There have been two main approaches in getting beyond plurality voting. In both cases, electors rank all of the candidates (unlike in plurality where only the most-preferred candidate is listed). In the first method, candidates get points based on their placements. For a 4 candidate election, every “first place” vote is worth 4, every second place vote is 3, and so on. The candidate with the most votes wins. In the second approach, the pairwise matchups are analyzed and the person who would win the most pairwise elections is deemed the overall winner. Ideally, there is a candidate who would win against any other candidate in a pairwise election, and that person is a natural choice for winner (and a choice that plurality is not guaranteed to choose). Such a candidate is known as a Condorcet winner.
I had always credited the foundation of these two approaches to Borda and Condorcet respectively. Both lived in the 1700s in France, Borda being a mathematician and military officer, Condorcet being a “pure” scientist and government official. But the real credit for these approaches should really go to Casanus and Llull four hundred years earlier. Numbers Rule gives a very good description of their work and all that was new to me.
One aspect of Numbers Rule that I really like is the brief biographical summary at the end of every chapter. Every chapter is based on one (or a few) key figures. Rather than try to weave the biography of that person in with the description of their findings in voting, only the key features are in the main text, while the biographical summary provides a deft summary of the rest of their lives. The people came alive through those summaries, but extraneous details did not hinder the main exposition.
The book is non-mathematical, in the that the very few equations are exiled to chapter appendices, but it is analytical in the sense that concepts are clearly and completely described. There is no hand-waving or “This is neat but really too hard for you”. Even NP-Completeness gets covered in a reasonable manner (in the context of my own work).
It is only in the coverage of my own work that I really disagree with the author. Briefly, Charles Dodgson (better known as Lewis Carroll of Alice in Wonderland fame) proposed that the winner of an election should be the one who becomes the Condorcet winner with the fewest number of changes to the electors’ ballots. Bartholdi, Tovey and I proved that determining the Dodgson winner is NP-Hard. Szpiro writes that this result was the “death knell” of Dodgson’s Rule, which I think vastly overstates the case. We solve NP-Hard problems all the time, through integer programming, constraint programming, dynamic programming, and practically any other -programming you like. There are very, very few practical elections for which we could not determine the winner of the election in a reasonable amount of time (exceptions would be those with a vast number of candidates). In my mind, the main problem with NP-Hard voting rules is that the losers cannot be succinctly convinced that they really lost. Without a co-NP characterization, losers have to be content with “The computer program I wrote says you lost”, which is unlikely to be satisfying. But I don’t think Dodgson’s rule is dead and I certainly don’t think I killed it!
Operations research comes out very well in the book. In addition to accurately describing Bartholdi, Tovey and me as Professors of Operations Research (kinda accurately: I was a doctoral student when the paper was written but an Assistant Professor at CMU when it was published), OR takes a star turn on page 189 when the work of Michel Balinski is described. Here is part of the description:
One of Balinski’s areas of expertise was integer programming, a branch of operations research. Developed before, during and after World War II, operations research originated in the military where logistics, storage, scheduling and optimization were prime considerations. But it soon acquired enormous importance in many other fields, for example in engineering, economics and business management. While game theory, developed at the same time, was mainly of theoretical interest, operations research was immediately applied to practical problems. Whenever something needed to be maximized or minimized – optimized for short – and resources were constrained, operations research offered the tools to do so.
What a lovely paragraph!
If you have any interest in learning about why voting and apportionment are not straightforward, and want a readable, history-oriented book on approaches to these problems, I highly recommend Numbers Rule: reading it has been a great way to spend a lazy weekend.
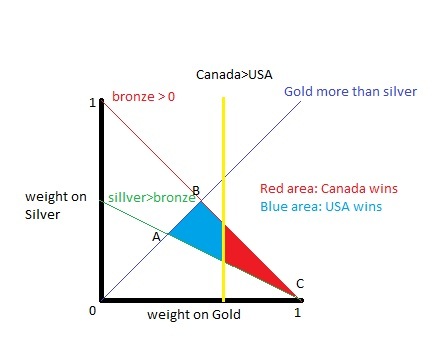In the Winter 2010 Olympics, Canada was edged out by the United States in the Trick Medal Championship (TMC) by a narrow margin. Canada had 14 gold, 7 silver, and 5 bronze; the US went 9, 15, 13. If you put enough weight on gold, then Canada wins. But only 45.25% of the reasonable weights put enough weight on Gold for Canada to win; the US wins for the remaining 54.75% of the weights.
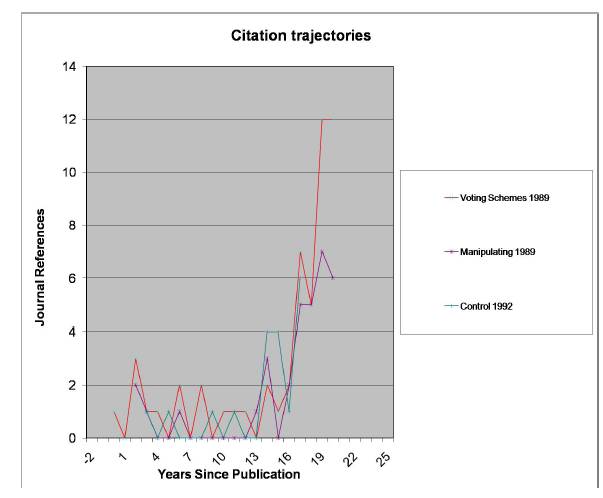But then something amazing happened about 5 years ago: people started referring to the papers! The references were mainly in computer science, but at least the papers were being recognized. The counts of these papers in the
The