I’m a sportswriter who is bound for the Olympics, and I’m writing an article about maximizing the number of events I see in a particular day.
I thought the input of a mathematician with expertise in these matters would be helpful to the story.
This was an interesting start to day a month ago. I received this email from New York Times reporter Victor Mather via University of Waterloo prof Bill Cook. Victor had contacted Bill since Bill is the world’s foremost expert on the Traveling Salesman Problem (he has a must-read book aimed at the general public called In Pursuit of the Traveling Salesman: Mathematics at the Limits of Computation). The TSP involves visiting a number of sites while traveling the minimum distance. While Victor’s task will have some aspects of the TSP, there are scheduling aspects that I work on so Bill recommended me (thanks Bill!).
Victor’s plan was to visit as many Olympic events in Rio as he could in a single day. This was part of a competition with another reporter, Sarah Lyall. Victor decided to optimize his day; Sarah would simply go where her heart took her. Who would see more events?
Victor initially just wanted to talk about how optimization would work (or at least he made it seem so) but I knew from the first moment that I would be optimizing his day if he would let me. He let me. He agreed to get me data, and I would formulate and run a model that would find his best schedule.
On the day they chose (Monday, August 15), there were 20 events being held. 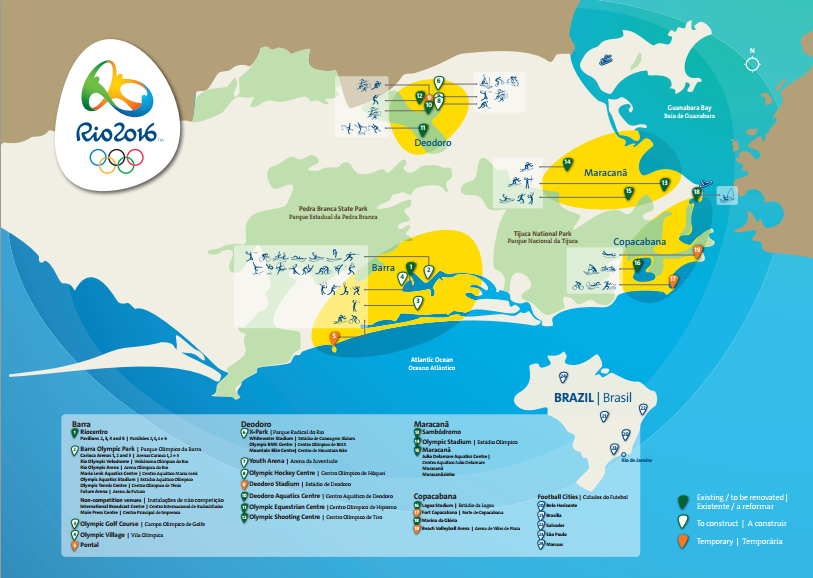 The map shows that the venues are all spread out across Rio (a dense, somewhat chaotic, city not known for its transportation infrastructure). So we would have to worry about travel distance. Victor provided an initial distance matrix, with times in minutes (OLY times). As we will see, this matrix must have been created by someone who had a few too many caipirinhas on Copacabana Beach: it did not exactly match reality.
The map shows that the venues are all spread out across Rio (a dense, somewhat chaotic, city not known for its transportation infrastructure). So we would have to worry about travel distance. Victor provided an initial distance matrix, with times in minutes (OLY times). As we will see, this matrix must have been created by someone who had a few too many caipirinhas on Copacabana Beach: it did not exactly match reality.
So far the problem does look like a TSP: just minimize the distance to see 20 sites. The TSP on 20 sites is pretty trivial (see a previous blog post for how hard solving TSPs are in practice) so simply seeing the sites would be quite straightforward. However, not surprisingly Victor actually wanted to see the events happening. For that, we needed a schedule of the events, which Victor promptly provided:
Badminton 8:30 am – 10:30 am // 5:30 pm -7
Basketball 2:15 pm – 4:15 pm// 7 pm -9 pm // 10:30 pm – midnite
Beach Volleyball 4 p.m.-6 p.m. // 11pm – 1 am
Boxing 11 am-1:30 pm, 5 pm – 7:30 pm
Canoeing 9 am – 10:30 am
Cycling: 10 a.m. – 11 am /// 4 pm – 5:30
Diving 3:15 pm -4:30
Equestrian 10 am- 11 am
Field Hockey 10 am – 11:30 am // 12:30 –2 // 6-7:30 pm // 8:30 pm -10
Gymnastics 2 pm -3 pm
Handball: 9:30 am- 11 am// 11:30 – 1pm //2:40 -4 //4:40 – 6 pm // 7:50 – 9:10 pm // 9:50 pm -11:10
Open water Swimming 9 am – 10 am
Sailing 1 pm – 2 pm
Synchronized swimming: 11 am- 12:30
Table tennis 10 am -11 am // 3pm -4:30 // 7:30pm – 9
Track 9:30 am -11:30 am // 8:15pm -10 pm
Volleyball 9:30 am- 10:30 am // 11:30 – 12:30 // 3pm – 4 pm // 5 pm – 6 pm // 8:30 pm -9:30 // 1030 pm -11:30
Water polo 2:10 pm – 3 pm // 3:30 -4:20 //6:20 -7:10 // 7:40 – 8:30
Weightlifting 3:30 – 4:30 pm // 7 pm- 8 pm
Wrestling 10 am – noon // 4 pm- 6 pm
Many events have multiple sessions: Victor only had to see one session at each event, and decided that staying for 15 minutes was enough to declare that he had “seen” the event. It is these “time windows” that make the problem hard(er).
With the data, I promptly sat down and modeled the problem as an mixed-integer program. I had variables for the order in which the events were seen, the time of arrival at each event, and the session seen for each event (the first, second, third or so on). There were constraints to force the result to be a path through the sites (we didn’t worry about where Victor started or ended: travel to and from his hotel was not a concern) and constraints to ensure that when he showed up at an event, there was sufficient time for him to see the event before moving on.
The objective was primarily to see as many events as possible. With this data, it is possible to see all 20 events. At this point, if you would like to see the value of optimization, you might give it a try: can you see all 20 events just by looking at the data? I can’t!
But there may be many ways to see all the events. So, secondarily, I had the optimization system minimize the distance traveled. The hope was that spending less time on the buses between events would result in a more robust schedule.
I put my model in the amazing modeling system AIMMS. AIMMS lets me input data, variables, constraints, and objectives incredibly quickly and intuitively, so I was able to get a working system together in a couple of hours (most of which was just mucking about with the data). AIMMS then generates the integer program which is sent to Gurobi software (very fast effective mixed-integer programming solution software) and an hour later I had a schedule.
| start | Arrival | Next travel time |
| canoe | 9:00 | 20 |
| open swimming | 9:35 | 45 |
| equestrian | 10:35 | 35 |
| wrestling | 11:25 | 10 |
| synchro | 12:15 | 30 |
| sailing | 13:00 | 30 |
| gymnastics | 14:00 | 10 |
| handball | 14:40 | 10 |
| basketball | 15:05 | 10 |
| diving | 15:30 | 10 |
| cycling | 17:00 | 30 |
| beach volleyball | 17:45 | 30 |
| badminton | 18:40 | 5 |
| boxing | 19:00 | 5 |
| weightlifting | 19:20 | 5 |
| table tennis | 19:40 | 10 |
| water polo | 20:05 | 35 |
| hockey | 20:55 | 35 |
| track | 21:45 | 20 |
| volley | 22:30 | |
| end | 22:45 |
This schedule has 385 minutes on the bus.
I discussed this problem with my colleague Willem van Hoeve, who spent about five minutes implementing a constraint programming model (also in AIMMS) to confirm this schedule. He had a access to a newer version of the software, which could find and prove optimality within minutes. Unfortunately my version of the software could not prove optimality overnight, so I kept with my MIP model through the rest of the process (while feeling I was driving a Model T, while a F1 racecar was sitting just up the hallway). CP looks to be the right way to go about this problem.
I spent some time playing around with these models to see whether I could get something that would provide Victor with more flexibility. For instance, could he stay for 20 minutes at each venue? No: the schedule is too tight for that. So that was the planned schedule.
But then Victor got to Rio and realized that the planned transportation times were ludicrously off. There was no way he could make some of those trips in the time planned. So he provided another transportation time matrix (olympics3) with longer times. Unfortunately, with the new times, he could not plan for all 20: the best solution only allows for seeing 19 events.
| Event | Arrival | Next Travel | Slack | |
| canoe | 9:00 | 30 | ||
| track | 9:45 | 45 | ||
| equestrian | 10:45 | 35 | ||
| synchro | 11:35 | 60 | 0:10 | |
| sailing | 13:00 | 60 | ||
| gymnastics | 14:15 | 15 | ||
| water polo | 14:45 | 15 | ||
| diving | 15:15 | 15 | 0:25 | |
| cycling | 16:10 | 15 | ||
| handball | 16:40 | 15 | ||
| wrestling | 17:10 | 25 | ||
| boxing | 17:50 | 15 | ||
| badminton | 18:20 | 15 | 0:10 | |
| weightlifting | 19:00 | 15 | 0:35 | |
| table tennis | 20:05 | 25 | ||
| basketball | 20:45 | 35 | 0:10 | |
| hockey | 21:45 | 45 | 0:30 | |
| volley | 23:15 | 30 | ||
| beach volleyball | 0:00 | |||
So that is the schedule Vincent started with. I certainly had some worries. Foremost was the travel uncertainty. Trying to minimize time on the bus is a good start, but we did not handle uncertainty as deeply as we could have. But more handling of uncertainty would have led to a more complicated set of rules and it seemed that a single schedule would be more in keeping with the challenge. The morning in particularly looked risky, so I suggested that Victor be certain to get to gymnastics no later than 2:15 in order to take advantage of the long stretch of close events that follow. Sailing in particular, looked to be pretty risky to try to get to.
I had other worries: for instance, what if Victor arrived during half-time of an event, or between two games in a single session? Victor probably wouldn’t count that as seeing the event, but I did not have the detailed data (nor an idea of the accuracy of such data if it did exist), so we had to hope for the best. I did suggest to Victor that he try to keep to the ordering, leaving an event as soon as 15 minutes are up, hoping to get a bit more slack when travel times worked out better than planned (as-if!).
So what happened? Victor’s full story is here and it makes great reading (my school’s PR guy says Victor is “both a reporter and a writer”, which is high praise). Suffice it to say, things didn’t go according to plan. The article starts out:
There are 20 [events] on the schedule on Monday. Might an intrepid reporter get to all of them in one day? I decide to find out, although it doesn’t take long to discover just how difficult that will be.
The realization comes while I am stranded at a bus stop in Copacabana, two and a half hours into my journey. The next bus isn’t scheduled for three hours. And I’ve managed to get to exactly one event, which I could barely see.
I had given him some rather useless advice in this situation:
“Something goes wrong, you reoptimize,” Professor Trick had cheerfully said. This is hard to do sitting on a bus with the computing power of a pen and a pad at my disposal.
Fortunately, he got back in time for the magical sequence of events in the afternoon and early evening. One of my worries did happen, but Victor agilely handled the situation:
Professor Trick urged me in his instructions to “keep the order!” So it is with some trepidation that I go off-program. Wrestling is closer to where I am than handball, and it looks like I will land at the handball arena between games. So I switch them. It’s the ultimate battle of man and machine — and it pays off. I hope the professor approves of my use of this seat-of-the-pants exchange heuristic.
I do approve, and I very much like the accurate use of the phrase “exchange heuristic”.
At the end Victor sees 14 events. 19 was probably impossible, but a few more might have been seen with better data. I wish I had used the optimization code to give Victor some more “what-ifs”, and perhaps some better visualizations so his “pen and pad optimization” might have worked out better. But I am amazed he was able to see this many in one day!
And what happened to Sarah, the reporter who would just go as she pleased? Check out her report, where she saw five events. If Victor went a little extreme getting a university professor to plan his day, Sarah went a little extreme the other way in not even looking at a map or a schedule.
This was a lot of fun, and I am extremely grateful to Victor for letting me do this with him (and to Bill for recommending me, and to Willem for providing the CP model that gave me confidence in what I was doing).
I’ll be ready for Tokyo 2020!
To quote the standard paraphrasing of a line from Helmuth v. Moltke: no operational plan ever survives contact with the enemy. (There’s also a version attributed to Napoleon: “The first casualty in any battle is the plan.”)
I wonder if the CP schedulers and the robust optimizers would like to get together and spawn a new field:robust constrained scheduling, maybe?
Nice job, Mike. I think the problem you tried to solve is a version of the “Team Orienteering Problem with Time Windows” (TOPTW) which I have recently come across with respect to a client that we’re working with. It’s not a Vehicle Routing Problem with Time Windows (VRPTW) because the VRPTW requires you to visit every site as a hard constraint. The idea in the TOPTW is that you collect a prize for each site you are able to visit.
At least in my limited literature review, the TOPTW (and even the VRPTW) are best solved with a variety of heuristics. So maybe there’s another racecar to consider. For the MIP and CP models, what would be interesting to know is how long it took each model to get a good feasible solution, without worrying about optimality.
The team orienteering problem has multiple people (“Find M paths…”) rather than just Victor, so this is more like a prize-collecting TSP with time windows. As for heuristics, that would have been the next step if optimization didn’t work. But it is pretty clear that Victor could have used a fast reoptimization heuristic!
I worked on a similar scheduling problem while I was at Bell Labs many years ago. My solution approach for this kind of problem is different and may be interesting to you. The number of events n is large but the number that one can visit in a day is much smaller, say k. Using the idea of color coding (due to Alon, Yuster and Zwick) one can get an algorithm with run-time of the form c^k poly(n) to find out if there is a tour that visit k events (here c is a fixed constant, about 4). In other words one can get a fixed parameter algorithm. This is quite practical for small k and we implemented a prototype for internal purposes.