Research – Page 2 – Mike Trick's Operations Research Blog

Operations Research Resolutions for 2012

It is the time of the year for resolutions. Resolutions help define what we would like to be, but are damned hard things to follow through on. As Paul Rubin points out, gyms will be overrun for a few weeks with “resolvers” (or, as my former personal trainer called them “resolutionists”) before the weight room empties again. I’ve been as guilty as any in this regard: it is no coincidence that my gym membership runs January 15-January 15 and that I renew it each year with the best intents, and the worst results. Paul suggests an OR view of resolutions:

…the New Year’s resolution phenomenon offers a metaphor for O. R. practice. The “resolver” diets, exercises, stops smoking or whatever for a while because the “boss” (their conscience) is paying attention. When the “boss” stops watching, the “resolver” makes excuses for why the new regime is too difficult, and reverts to previous behavior. An O. R. solution to a business problem that is implemented top-down, without genuine commitment by the people who actually have to apply the solution (and change behaviors in doing so), is likely to end up a transient response leading to a return to the previous steady state.

So, in keeping with an operations research view of resolutions, I’ve been thinking about my resolutions with a particular focus on variables (what choices can I make), constraints (what are the limits on those choices) and objectives (what I am trying to accomplish). It does no good to define objectives and go willy-nilly off in those directions without also defining the constraints that stop me from doing so. But, of course, a creative re-definition or expansion of variables might let me find better solutions.

I have personal resolutions, and take inspiration from people around me who are able to transform themselves (yes, BB, I am talking about you!). But I also have some professional resolutions. So, here they are, and I hope they have been improved by an operations research view:

Make time for research. This might seem to be a funny resolution: isn’t that a big part of what professors do? Unfortunately, I have taken an administrative role, and there is a never-ending list of things to do. Short term, it seems if I will be a better Associate Dean if I get on with the business of Associate Deaning, but long-term I know I will be a better Associate Dean if I keep active in research. The decision model on time allocation has to be long term, not short term.
Do what makes me happiest. But where will the time come from? I need to stop doing some things, and I have an idea of what those are. I have been very fortunate in my career: I’ve been able to take part in the wide varieties of activities of a well-rounded academic career. Not all of this gives me equal pleasure. Some aspects (*cough* journals *cough*) keep me up at night and are not my comparative advantage. So now is the time to stop doing some things so I can concentrate on what I like (and what I am comparatively good at). While many of my decisions in my life can be made independently, time is a major linking constraint.
Work harder at getting word out about operations research. This has not been a great year for this blog with just 51 posts. I don’t want to post just for the sake of posting, but I had lots of other thoughts that just never made it to typing. Some appeared as tweets, but that is unsatisfying. Tweets are ephemeral while blog entries continue to be useful long after their first appearance. This has been a major part of my objective function, but I have been neglecting it.
Truly embrace analytics and robustness. While “business analytics” continues to be a hot term, I don’t think we as a field have truly internalized the effect of vast amounts of data in our operations research models. There is still too much a divide between predictive analytics and prescriptive analytics. Data miners don’t really think of how their predictions will be used, while operations researchers still limit themselves to aggregate point estimates of values that are best modeled as distributions over may, predictable single values. Further, operations research models often create fragile solutions. Any deviation from the assumptions of the models can result in terrible situations. A flight-crew schedule is cheap to run until a snowstorm shuts an airport in Chicago and flights are cancelled country-wide due to cascading effects. How can we as a field avoid this “curse of fragility”? And how does this affect my own research? Perhaps this direction will loosen some constraints I have seen as I ponder the limits of my research agenda.
Learn a new field. While I have worked in a number of areas over the years, most of my recent work has been in sports scheduling. I started in this are in the late 90s, and it seems time to find a new area. New variables for my decision models!

OK, five resolutions seems enough. And I am not sure I have really embraced an operations research approach: I think more constraints are needed to help define what I can do, my objective is ill-defined, and even my set of variables is too self-limited. But if I can make a dent in these five (along with the eight or so on my personal list) then I will certainly be able to declare 2012 to be a successful year!

Happy New Year, everyone, and I wish you all an optimal year.

This entry is part of the current INFORMS Blog Challenge.

That’s got to be true… doesn’t it?

Back in 1996, Harvey Greenberg, longtime faculty member at the University of Colorado at Denver, began putting together a collection of myths and counterexamples in mathematical programming. While generally I find mathematical programming to be quite intuitive, there turn out to be lots of things that I think must be true that are not. Consider the following:

The duality theorem applies to infinite LPs.
Simulated annealing converges more slowly than steepest descent when there is a unique optimum.
In linear programming, a degenerate basis implies there is a (weakly) redundant constraint.
If f has continuous nth-order derivatives, local behavior of f can be approximated by Taylor’s series.
The problem of finding integer x such that Ax = b, where A is an m by n integer matrix and b a length m integer vector, is NP-complete.

Amazingly none of these are true! Reading through the myths and counterexamples reminds me of how much I “know” is really false.

The Myths and Counterexamples document is hosted by the INFORMS Computing Society as part of its Mathematical Programming Glossary, and Harvey periodically updates the Myths site (with the last update being in February 2010). If you have shown that something that seems obvious is actually false, be sure to let Harvey know about it. And the next time you are doing a proof and are tempted to make a claim because “it is well known that…” or “obviously…”, perhaps you should check out the site first.

Thanks to @fbahr and the folks at Reddit’s SYSOR for reminding me of the value of a project I have followed for about fifteen years so far!

Postdocs and Special Year at the IMA

In 1987-88, I spent a great year in Minneapolis as a postdoc at the Institute for Mathematics and its Applications (and this picture of me comes from that time). Every year at the IMA has a special theme, and the theme my year was “Applied Combinatorics”. There were about a dozen of us postdocs that year: 11 combinatorialists, and me, the OR guy, who I guess satisfied the Applied in year’s title. It was a fantastic year. The other combinatorialists were scary-smart and doing amazing things. One of the postdocs was Bernd Sturmfels who was working on Grobner Bases at the time and has gone on to an amazing career in applying algebraic methods in optimization, statistics, and other fields. I look at his list of 190 papers and 15 books and realize what a slacker I am!

The year at the IMA was important for my career. It gave me the chance to finish my dissertation papers and move on to new research. I met a great group of people and learned about some aspects of an academic career without being saddled with teaching or administrative duties.

Depending on the year, the IMA may be more or less interesting to operations researchers. Next year (2011-12) looks to be a good one. It is on “The Mathematics of Information”. There are a couple versions of the description of the year. I like the one on the Geomblog:

During the academic year 2011-2012, the annual program at the Institute for Mathematics and its Applications (IMA) at the University of Minnesota will be in the Mathematics of Information. Information, broadly defined, plays an ever increasingly large role in our scientific and technological endeavors, as well as our daily lives. Collectively, we search the web over billions of times per day, we keep our medical records in digital repositories, we share videos and photos over the web, and we listen to music on MP3 players. Our ability to collect, store, and generate vast quantities of data far outstrips our ability to analyze, process, and understand these data. Many scientific, engineering, and medical applications depend on our ability to handle enormous amounts of complex information. Network engineering involves massive datasets at high speeds, medical imaging generates large data with intricate geometric relationships, and astronomical observations include data at different wavelengths or spectral bands. Our current technology and scientific tools for information lag far behind our ability to collect enormous amounts of data, our need to analyze that data as efficiently as possible, and, finally, our ability to use that analysis to make sound, timely decisions.

“Sound, timely decisions” is what operations research is all about.

The postdoc deadline was January 7, 2011 but applications will be considered until February 4, 2011. So get a move on if you are interested!

There is also funding for more established researchers to spend time at the IMA. It is a great way to get started in new research directions and to rub off the administrative barnacles that attach if you stay at one place too long.

The Sexiness of Integer Programming

Suresh Venkatasubramanian, of the excellent Geomblog, is at SODA and covered some preconference conferences. When covering a paper that used integer programming (via CPLEX), his comment was:

It’s not the “sexiest” thing in the world to solve algorithms problems in practice by using large industrial strength packages.

Oh, he didn’t say that, did he?

I spend most of my life “solving algorithms problems in practice by using large industrial strength packages”. I solve sports scheduling problems, logistics problems, and even problems in social choice with large scale integer programming software as my primary tool. Who says I am not sexy? Or, worse, that my research is not sexy?

I can think of a few misconceptions that might lead one to doubt the sexiness of integer programming.

Integer Programming is uncreative. After all, you just formulate the problem in terms of variables, linear objective, and linear constraints, toss it in a code, and you are done. Where is the research?
Such a view ignores the tremendous number of choices once must make in formulating integer programming. The choice of variables, constraints, and objective can have a tremendous impact on the effectiveness of the solver. While solvers continue to get better at automatically identifying formulation improvements, formulating integer programs is still an art. It is an art, however, enhanced by theory. As we better understand the polyhedral characteristics of integer programming formulations, we create better and better formulations.

This creative effort is expanded when alternatives to “basic” formulations are included. Creating a branch-and-price, branch-and-cut, Benders, or other type of formulation can be the key to solving real problems, but may require significant research effort.
Integer programming is slow. This seems to be the most common response I get from those outside the integer programming subfield. One quote from a person at a well-known computer science-oriented firm: “I tried integer programming. It doesn’t work.” Not “It doesn’t work for this problem” or “I couldn’t make it work”. Just “It doesn’t work”. How can a topic be sexy if it doesn’t work?
I think one of the great stories in all of mathematics and business is the incredible confluence between increased data, faster computers, algorithmic improvements, and implementation successes that have led to many orders of magnitude speed increases in integer programs. Over the last fifteen years, we have gotten much, much better at solving integer programming models. With the underlying linear programming solvers being more than million times faster (no hyperbole: both computers and algorithms provide more than a 1000 time speedup each), lots of instances formerly out of reach can now be solved routinely.

Of course, integer programming is exponential time in the worst case. But I am not sure why a polynomial time algorithm that gets an approximate solution within a factor of, say, 42 is any “sexier” than an algorithm that finds the optimal solution in a reasonable amount of time for any instance of practical import.
Integer programming is expensive. Hey, if you have to spend tens of thousands of dollars for solutions, that really doesn’t count does it? It is like a troll dressed up in a $5,000 suit: it might look OK, but it’s not sexy!
No one has to pay a lot for high quality integer programming software. Suresh refers to this in his post:

This was surprising to me on two levels: firstly, that CPLEX is actually free for academic use (who knew!) and that such a simple approach is so effective.

Actually, all the major programs offer a way for free academic use. I particularly like Gurobi’s approach, which is based on periodic validation through a “.edu” domain, but academics can also get CPLEX (as you would have read on my blog last year) and XPRESS.

And if you are not an academic? COIN-OR offers “industrial strength” linear and integer programming in an open source approach.

In Suresh’s defense, here is the full quote, where he makes clear his support for this type of research:

It’s not the “sexiest” thing in the world to solve algorithms problems in practice by using large industrial strength packages. However, both CPLEX and SAT solvers are examples of tools that can be used in practice to solve fairly intractable problems. It still takes a lot of engineering and skill to make the heuristics work well, but it’s something that we should be using as a matter of course when designing heuristics before trying to invent an algorithm from scratch.

Suresh obviously gets it: let’s hope his post expands interest in integer programming methods for these problems.

Integer programming is useful, fast, and cheap. If that isn’t sexy (for an algorithm!), then I don’t know what is.

Some Older but Perhaps Useful Notes on Networks and Matchings

More than 20 years ago, I was a postdoc at the Institut für Ökonometrie und Operations Research at the University of Bonn, an Institute headed by Prof. Bernhard Korte (who now heads Bonn’s Research Institute for Discrete Mathematics). It was a fantastic year. Also visiting that year were people like Bill Cunningham, Bill Cook, Andras Sebo, and many others. I learned a lot that year, and many aspects of what I learned showed up in my future research. I was fortunate that I had a position at Carnegie Mellon but was allowed to delay the start by a year so I did not have to worry about job hunting during that time.

I loved living in Bonn. Though I spoke no German at the beginning and very little by the end, I had a great time there, bicycling around and exploring the various areas of the town. It helped that I met Ilona, who would go on to be my wife, so we could share those explorations (and she could handle all the German things).

During the year, I taught a Ph.D. seminar on networks and matchings. In the course of the seminar, I put together some notes on the topic, amounting to about 80 pages of material. I recently came across the files for those notes, and am very impressed with the younger me: I seemed to have a lot of time available during that period. The notes are in an interesting format. All the results (which are mainly proofs of correctness or algorithmic analysis) are broken into digestible pieces. So, rather than ask “What is the complexity of this algorithm”, the result is broken down into a number of steps, leading up to the result. I was trying to recreate the thought process that went into the proofs in the hope that would make it easier for students to follow and emulate. It seemed to inspire at least some students: two students (Thomas and Helga, who I would see periodically in the following years) brought together my notes and presented me with a bound copy at the end of the course, a copy I still keep proudly on my shelves.

I am not sure the value of 20 year old notes. Some basic algorithms haven’t changed in that time of course: Dijkstra’s shortest path, Edmonds and Karp’s max flow algorithm, and so on. Other approaches have been supplanted in the intervening time, and certainly books like Ahuja, Magnanti, and Orlin’s Network Flows covers more material and more depth. But having found my notes, I would not like to see them lost again, so here they are in case anyone finds them useful. The way the notes were designed to be used, students would get a version without the boxed answers and would try to work through the problems on their own. If I find the tex source, I’ll see if I can add a student version: this is the instructor’s version.

Notes on Network Flows and Matchings by Michael Trick

Bus Bunching talk at INFORMS

New post at the INFORMS site: “Avoiding Bunches of Buses”:

While the INFORMS conference is big enough to stay within a narrow research area, it is also a great place to get inspiration outside your focus. I hopped in to see a talk given by Don Eisenstein on work he has done with John Bartholdi on “scheduling” buses. Don and I were in graduate school together, and we each had John as our advisor, but we work in completely different areas.

Don talked about a system they have put in place to handle buses, trollies, and other transportation systems that have multiple vehicles going over the same routes. I am sure we have all had the frustration of waiting a long time for a bus, only to have three buses (all running the same route) appear in quick succession. This phenomenon is common enough to form the title for a popular mathematics book. Upon reflection, this situation is not mysterious. If buses are scheduled on a route at, say, 10 minute intervals, then any delay in one bus (a slow entering customer, a traffic jam, and so on), will cause that bus to run even later. Once delayed by two minutes, more passengers will arrive in the now-12 minute gap, further slowing down the bus. Meanwhile, the bus following the delayed bus will go faster than normal due to a dearth of passengers for it. Very quickly, a small increase in the gap will turn into a large gap ahead of the delayed bus and a small gap behind it.

This bunching behavior is very common, and very difficult to schedule around. In fact, as buses try to keep to the schedule, drivers may resort to dangerous or illegal driving, particularly if drivers are evaluated by their ability to keep to a schedule. This situation is made worse if a bus suffers a mechanical failure, leading to a large gap in the schedule until the bus can be replaced.

Overall, trying to keep a bus system running smoothly is a very difficult problem. Lots of people have tried to create better, more robust schedules, but such systems are often complicated and difficult to implement.

John and Don propose a very simple method for handling such a system. The idea is to have a small number of checkpoints in the system (in the example they chose, they had a checkpoint at each end of the route, with the bus going back and forth along the route). When a bus hits a checkpoint, the system checks how far behind the next bus is. If the next bus is expected to hit the checkpoint in 10 minutes, say, then the current bus waits a fixed fraction of that 10 minutes (say .6 times the following time, or six minutes in this case) and then departs. There is a variant when a bus waits at least, say, 3 minutes after the preceding bus had hit the checkpoint. That is the entire system! Ignore schedules, but simply wait a fixed fraction of the time before the next bus arrives.

This simple system has the amazing property that it will self-organize into a nicely spread-out arrangement of buses, and will reorganize itself in the face of bus delays (or speed-ups). If a bus goes out of operation, nothing special needs to be done: the system will automatically move the buses into a evenly spread-out pattern (albeit longer apart, since there are fewer buses). Of course, it also gives up on a fixed schedule, but for systems that arrive often enough, the schedule is generally not relevant to passengers (and in the example they gave, only known to the drivers, not to the passengers).

This research follows their previous work on self-organizing manufacturing systems. The thing I like very much about this entire research direction is how well it includes robustness. While simple, these self-organizing systems respond extremely well to changes in the environment, much better than many optimization approaches.

The presentation was very convincing, and Don and John promise a paper “in a few weeks”. I look forward to reading it in more detail (and perhaps correcting any errors in interpretation I have of their work).

This was just one of the thousands of talks at this conference. I was very glad I went outside of my normal research range to see this talk.

A New Approach to MaxFlow?

The MIT public relations office is reporting a new result on the maximum flow problem. It appears that work by Kelner, Madry, Christiano, Spielman and Teng (in some permutation: not surprisingly, the MIT release stresses the MIT authors) has reduced the complexity of maxflow to (V+E)^4/3 (from (V+E)^3/2. Details are pretty sketchy, but the approach seems to use matrix operations instead of the more combinatorial “push flow along this path (or edge)”. From the announcement:

Traditionally, Kelner explains, algorithms for calculating max flow would consider one path through the graph at a time. If it had unused capacity, the algorithm would simply send more stuff over it and see what happened. Improvements in the algorithms’ efficiency came from cleverer and cleverer ways of selecting the order in which the paths were explored.
But Kelner, CSAIL grad student Aleksander Madry, math undergrad Paul Christiano, and Professors Daniel Spielman and Shanghua Teng of, respectively, Yale and USC, have taken a fundamentally new approach to the problem. They represent the graph as a matrix, which is math-speak for a big grid of numbers. Each node in the graph is assigned one row and one column of the matrix; the number where a row and a column intersect represents the amount of stuff that may be transferred between two nodes.

In the branch of mathematics known as linear algebra, a row of a matrix can also be interpreted as a mathematical equation, and the tools of linear algebra enable the simultaneous solution of all the equations embodied by all of a matrix’s rows. By repeatedly modifying the numbers in the matrix and re-solving the equations, the researchers effectively evaluate the whole graph at once.

I am a little hesitant here, since I can’t find the relevant paper. Worse, the presentation abstract talks about approximate maximum flow (see the September 28 entry at the MIT seminar listing), which would then add in some extra terms for exact max flow. So I welcome more information on the result.

In any case, it is exciting to see a new approach to these sorts of problems. If past experience is any guide, if this approach is workable, we can expect to see an avalanche of papers applying the approach to all sorts of network flow problems: shortest path, min cost flow, generalized networks (with multipliers) and so on. A likely good place to start is this overview paper by Spielman.

Definitive Word on P!=NP Paper

Lance Fortnow of the blog Computational Complexity has, I believe, the definitive word on the P!=NP paper by Deolalikar (saying in a sentence what I couldn’t quite manage in two pages):

Proving P ≠ NP will require pure genius but you shouldn’t need a Fields medalist to verify the proof.

Secondary message: a good way to determine if a proof will work is to count the “clearly”s and “should be able to”s: more than one or two and the proof likely will fall apart at the slightest breath.

P versus NP and the Research Process

By now, everyone in computer science and operations research is aware of the purported P<>NP proof of Vinay Deolalikar of HP Labs. After intense discussion (mainly through blogs and wikis), the original paper was taken down, and Vinay has prepared a new version for submission. He claims:

I have fixed all the issues that were raised about the preliminary version in a revised manuscript (126 pages); clarified some concepts; and obtained simpler proofs of several claims. This revised manuscript has been sent to a small number of researchers. I will send the manuscript to journal review this week. Once I hear back from the journal as part of due process, I will put up the final version on this website.

I am convinced by Dick Lipton’s blog entry and by Scott Aaronson’s commentary suggesting fundamental flaws in the paper, but since Vinay has not retracted the paper, I will look forward to the definitive version of the paper. For a detailed description of the issues, press coverage, and other aspects, polymath has an extensive wiki on the topic.

What I find most intriguing is the field’s response to this claimed proof. Proofs that P=NP or P<>NP are certainly not uncommon. Gerhard Woeginger faithfully keeps track of these claims and is up to 62 in his list. Some of these results come out of the operations research world. For instance, Moustapha Diaby is a faculty member at the business school at the University of Connecticut and believes he has found linear programming formulations for NP-hard problems (number 17 on Woeginger’s list).

The Deolalikar paper is unique, however, in that many, many top mathematicians looked very closely at the paper and worked very hard to determine its correctness. This group includes people like Fields-medal winner Terrence Tao and Polya and Fulkerson prize winner Gil Kalai. Why did so many very smart people (and successful! They don’t do wikipedia pages on just anyone [yet]) spend time on this while practically no one spends time with the other 61 purported proofs?

The most obvious reason is that this paper presented a fundamentally new approach to this problem. As Lipton says: “the author has advanced serious and refreshingly new ideas of definite value”. In this proof, Deolalikar uses finite model theory, an area of logic, to deduce structures in random satisfiability problems. If P=NP, then the structures would have to be different than what is already known about random satisfiability problems in the critical region (this synopsis is vague to the point of not being usable). This is definitely a different direction than past efforts, bringing together a number of disparate fields.

Further, Deolalikar knows very well that there are a number of proofs in the literature that say “P<> NP cannot be proved this way”. For instance, any result that cannot distinguish between the easy 2-satisfiability and the hard 3-satisfiability is doomed to failure (Aaronson’s blog entry gives a few others along with other signs to check for in claimed proofs). Deolalikar presented reasons for believing that his approach evaded the barriers. This leads to excitement! Could this approach avoid known invalid approaches?

Contrast this with papers that suggest that a linear programming model can correctly formulate an NP-complete problem. Yannakakis showed that no symmetric formulation can do so, and that provides a powerful barrier to linear programming formulations. Not only must a a formulation not be symmetric, but its asymmetry must be of the sort that continues to evade Yannakakis’ proof. Without a strong argument on why an LP formulation fundamentally avoids Yannakakis’ argument, it is not even worthwhile spending time with LP formulations of NP-complete problems.

This overwhelming doubt was clearly not felt by some referees who allowed Diaby’s papers to be published in “International Journal of Operational Research”, lending credence to the idea that the refereeing and journal process in operations research is broken (in my view, of course). For the steps given in the Computational Complexity blog, we have have to add a step: “Your paper is accepted by a third tier journal and still no one believes it.” Similarly, it will not be enough for me to see that Deolalikar’s paper is published: at this point I trust the blogs (some of them, anyway) more than the journals!

Even if the Deolalikar result is shown not to be valid, the paper gives me enormous hope that someday the P<>NP (as I believe it is, rather than P=NP) will be proved. We appear to be developing methods that will have some traction in the area.

Algorithmic Voting Theory, Venice, and a Talk on Old/New Papers

I just got back from Venice, where I attended a conference on Algorithmic Decision Theory. This is a new conference series (optimistically numbered the first conference, implying at least a second) revolving around issues in uncertainty in decision making, preference solicitation, learning and other issues. From the conference web page:

A new unique event aiming to put together researchers and practitioners coming from different fields such as Decision Theory, Discrete Mathematics, Theoretical Computer Science and Artificial Intelligence in order to improve decision support in the presence of massive data bases, combinatorial structures, partial and/or uncertain information and distributed, possibly inter-operating decision makers. Such problems arise in several real-world decision making problems such as humanitarian logistics, epidemiology, risk assessment and management, e-government, electronic commerce, and the implementation of recommender systems.

This area has been very active, particularly in computer science where there are a host of applications.

I was asked to give one of the invited talks, and spoke on “An Operations Research Look at Voting”. I was a little worried about giving this talk, since my main qualifications come from papers published twenty years ago. When I was a doctoral student at Georgia Tech, I worked with John Bartholdi and Craig Tovey on computational issues in voting. Being the first to look at those issues, we got to prove some of the basic results in the area. These include

For some natural voting rules, it is NP-hard to determine who the winner is.
For some natural voting rules, it is NP-hard to determine how to manipulate the rule (where manipulation means misrepresenting your preferences so as to get a preferred outcome).
For some natural voting rules, optimally using the powers of a chair to form subcommittees or otherwise manipulate the voting process is NP-hard.

We published this work in Social Choice and Welfare (after getting it rejected from more mainstream economics journals) where … it was soundly ignored for 15 years. No one referred to the papers; no one followed up on the papers; no one cared about the papers at all!

This work was my job talk in 1987/88, and it got me a wonderful job here at the Tepper School (then GSIA), Carnegie Mellon. And, without Google Scholar, it was not obvious that the papers were being ignored, so they added to my vita, and made it a bit easier to pass through the various steps.

But I did like the work a lot, and regretted (and still regret) that my economist colleagues did not take computational limits more seriously in their models.

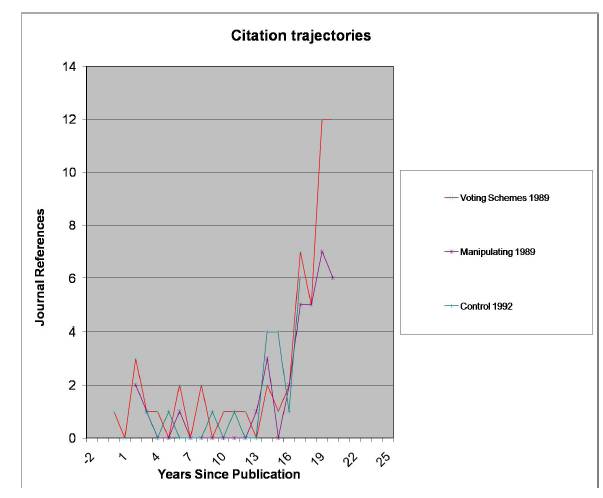votingcites But then something amazing happened about 5 years ago: people started referring to the papers! The references were mainly in computer science, but at least the papers were being recognized. The counts of these papers in the Web of Science (formerly Science Citation Index) are particularly striking. In the associated graph, the x-axis is years since publication; the y-axis is the number of references in Web of Science in that year (Google scholar numbers are higher of course, but there is a bias towards more recent papers there). In my talk, I compare that graph to my “normal” papers, which reach a peak after 4 or 5 years then decrease. It is really gratifying to see the interest in these papers along with all the really cool new results people are getting.

I closed off the talk with some work I have done recently on creating voting trees. Suppose there are three candidates, “a”, “b”, and “c”, and you really like candidate “a”. Many voting systems proceed as a series of comparisons between two alternatives (think of standard parliamentary procedure). If you are the chairperson, you might try to bring the candidates forward so as to increase the chances of “a” winning. In fact, if you set the agenda to be “b” against “c” and the winner against “a”, then “a” will win as long as “a” beats someone (and no one beats everyone). In this problem, the goal is to do the manipulation without knowing other voters’ preferences.

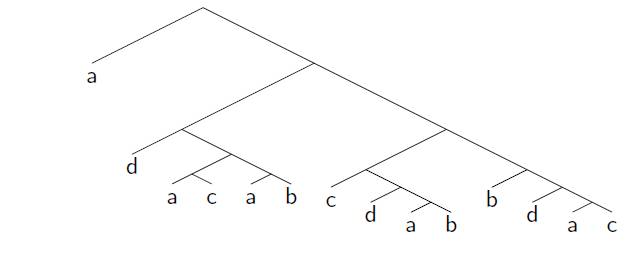lextree4 Can you do this for four candidates? If you want “a” to win, “a” must be in the top cycle: the group of candidates (perhaps the entire set of candidates) who all beat all the other candidates. The “Condorcet winner” is the minimal top cycle: if some candidate beats all the other candidates one-on-one, then that candidate must win any voting tree it occurs in. So, assuming “a” is in the top cycle, can you create a voting tree so that “a” wins with four candidates? The answer is yes, but it is a bit complicated: first “a” goes against “c” with the winner against “d” then the winner against “b” who plays the winner of (“a” goes against “b” with the winner against “d” …) …. actually, the minimum tree has 14 leaves! I am biased, but I think the tree is beautiful, but it goes to show how hard it is to manipulate agendas without knowledge of others’ preferences. I am in the process of generating the trees on 4 candidates: there is a very natural rule (“Copeland winner with Copeland loser tie break”: see the presentation for definitions) that requires more than 32 leaves (if an implementation tree for it exists).

Sanjay Srivastava and I made a conjecture almost 15 years ago that would imply that this sort of manipulation would be possible no matter how many candidates. Little progress has been made but I think it is still a great problem (the economists know this as implementation by backwards induction and characterizing rules implementable on trees is an important problem in social choice/mechanism design).

If you want more details on all this, here are my slides. The references are

Small Binary Voting Trees M.A. Trick, Small Binary Voting Trees, First International Workshop on Computational Social Choice,
Amsterdam, Netherlands, 500-511 (2006).
Sophisticated Voting Rules S. Srivastava and M.A. Trick, Sophisticated voting rules: The two tournament case, Social Choice and
Welfare, 13: 275-289 (1996).

How hard is it to control an election?, with C. A. Tovey and M. A. Trick. A slightly revised version of this appeared in Mathl. Comput. Modelling (Special Issue on Formal Theories of Politics) 16(8/9):27-40 (1992).

The computational difficulty of manipulating an election, J.J. Bartholdi, C. A. Tovey and M. A. Trick (1989); Social Choice and Welfare 6:227-241 (1989).
Voting schemes for which it can be difficult to tell who won the election, J.J. Bartholdi, C. A. Tovey and M. A. Trick; Social Choice and Welfare 6:157-165 (1989).

Oh, and Venice is a beautiful place to visit. But you might have heard that elsewhere.