Category: Personal

Continuing to be impressed with the 28 year old me

In the wake of coming across my network and matching notes, where the 28 year old me taught the 50 year old me some things I never realized I knew, in a way that leaves (the 50 year old) me breathless (at least about the amount of time the 28 year old me had), I was delighted to see a new survey (published in the Communications of the ACM, no less) about complexity and voting systems that says some very nice things about the 28 year old me.    The article, written by Piotr Faliszewski, Edith Hemaspaandra, and Lane Hemaspaandra looks at elections and the well known issue of manipulation of elections by giving untruthful representations of one’s preferences.  The authors survey approaches that use computational complexity to protect elections:

This article is a nontechnical introduction to a startling approach to protecting elections: using computational complexity as a shield. This approach seeks to make the task of whoever is trying to affect the election computationally prohibitive. To better understand the cases in which such protection cannot be achieved, researchers in this area also spend much of their time working for the Dark Side: trying to build polynomial-time algorithms to attack election systems.

I have a particular fondness for this issue, since the 28 year old me (and his coauthors) wrote about this:

This complexity-based approach to protecting elections was pioneered in a stunning set of papers, about two decades ago, by Bartholdi, Orlin, Tovey, and Trick.  The intellectual fire they lit smoldered for quite a while, but in recent years has burst into open flame.

Wow!  Now that is a paragraph to send off to my Dean!  I have written about how this approach was ignored for a long while, but is now pretty popular.  It is great to see this coverage in an outlet like CACM.

The article goes on to survey this area, and has lots of nice things to say about those 20 year old papers (“seminal” (twice!), “striking insight”).  And it makes a great case for all the work that has been done since, and issues going forward.  Thanks Piotr, Edith, and Lane:  I enjoyed the survey very much.  And my Dad is visiting, and he too loved reading about what my coauthors and I had done.

From the 50 year old me to the 28 year old me:  “That was pretty good work!”  And, if I can speak for the 28 year old me:  “Thanks!  What are you doing now?” 50 year old me: “Hmmm….. can I tell you about sports scheduling? Blogging? Or perhaps I should introduce you to Alexander?”.  28 year old me: “Wasn’t I the one who met Ilona, with whom you have Alexander?”  50 year old me: “OK, we’ll split that one!”

Different phases, different measures.  But I am impressed with the 28 year old me every time I run across him.

Yet More Tag Clouds

@polybot on twitter pointed to the Tagxedo site, a site that creates displays of words, kinda like Wordle.  There are a zillion choices (and even a presentation on 101 things you can do with Tagxedo).  Here are a few I generated while Alexander did homework and I watched football on a rainy Sunday.

What is operations research?  (based on the words in this blog)

What am I tweeting about?

Who am I (from my home page, it is not obvious but the background is a picture of me)

Here are words from the biographies of my twitter followers:

I don’t know if they mean anything, but they are fun to play with!

ALIO/INFORMS Talk on Benders

My talk at the ALIO/INFORMS Conference in Buenos Aires was on combinatorial benders’ approaches to hard problems.  I really think this approach is an important one that is not yet utilized enough.  You can get the talk here (apologies for the powerpoint:  I wanted to convert to beamer but was too latex-stupid to get things done quickly enough).  A paper on benders for sports scheduling is here, while one for transportation planning will be added when I get back.

The talk went well, I thought:  people seemed engaged, and I had fun giving the talk.  No wireless mike, so I opted to go without a microphone, so I hope those in the back could hear me.  Generally I prefer if people use microphones, but this was not the first time I did not take my own advice.

Off to Buenos Aires

I am off on Friday to Buenos Aires (via Atlanta)  for the ALIO/INFORMS conference.  I am giving a tutorial Monday on combinatorial Benders’ approaches and am tearing my hair out trying to get a structure to the talk.

If anyone else is going down (particularly a fellow blogger), drop me a note:  we can do a “Bloggers (and Readers) Beer” together.

I’ll try to blog some of the interesting activities at the conference:  INFORMS doesn’t seem to be organizing things the way they do at the annual meeting so the blogging will be a bit more informally done.

Martin Gardner has Passed Away

Martin Gardner has passed away.  I know I am not the only person in operations research who was inspired by Gardner’s Mathematical Games columns in Scientific American.  I have a strong memory of whiling away long high school physics classes reading Gardner’s columns (and thankful that patient and insightful physics teacher had a stack of Scientific Americans and did not mind my lack of attention to his teaching).  A large number of the columns were really about operations research problems:  “What is the best way to do this?”  “How few moves are needed to accomplish that?”  It is through his columns that I understood the breadth and beauty of mathematics, and how that world was accessible even to a high school student.  And that high school students and professional mathematicians could work on the same problem and each have something to contribute.

When I went to university, it took me some time to find the type of mathematics that inspired what Gardner inspired.  I found it in operations research, and I am thankful for Martin Gardner for showing me what to look for.

Google Maps API Enhancements

Google just announced some enhancements to their Directions in Maps API.  One addition, “avoiding tolls and highways” doesn’t really affect me much:  we have only one toll road in the area, and it is pretty well needed to go either east or west.  But the other two are exciting!

First, the API now adds bicycle routing.  I don’t know if it will let you go the wrong way down one way streets or hop on a crowded sidewalk to make a shortcut, but it does contain at least some of the long-distance bike paths.  Check out the path from my house to my buddy Barack’s place.  There is a bike path starting from about 20 miles from Pittsburgh all the way to Washington, DC.  I turn 50 this year, and have promised myself that I will do that trip.  Of course, I have broken promises before, and if I don’t start training soon, it won’t happen.  But it is nice to see Google will be by my side if I do set off.

The second, and more relevant to OR, enhancement adds Traveling Salesman routing capability.  From the announcement:

Route optimization. Have many places to go but no preference as to the order you visit them in? We can now reorder the waypoints of your route to minimize the distance and time you must travel. Very useful for traveling salesman I hear.

Now I would love to experiment with this!  There have been similar efforts before.  Gebweb has offered routing since 2007, and promises optimal solutions for up to 15 cities with 2-opting solutions for larger problems.  I would love to know how far Google guarantees optimality before resorting to a heuristic (the demo on the announcement page limits you to 11 points).  Unlike the other additions, this has not yet made it to Google Maps, but when it does, let’s see how Google competes with Concorde.

Yo Trick! Where’ve you been?

I was annoyed at myself this morning when I realized that January was almost over and I had only 3 blog posts.  Since my goal is 3/week, it is clear that I am getting the year off on the wrong foot.   I could, of course, put in eight or so posts on being too busy to post (kinda like a tweet I had about being too busy to tweet!) but I don’t think my audience would fall for that:  being OR people, they are pretty smart and can see through such an obvious ploy.

But it has been an interesting month, so I thought I would update on some of things that are happening in my life.  Perhaps this will also help with the question “What does a faculty member do all day long?”

I’ll begin with teaching, since this is a pretty heavy teaching period, with two courses and three sections:

The first course is “Mining Data for Decision Making”, a course that I created back in 2000 for our MBA students.  This course is extremely popular with the MBAs and I ended with with full classes (80 students each) for the two sections, with about 40 on the waiting list.  After a couple less-than-stellar lectures, I got it whittled down to 7 left on the waiting list by the time the add-drop deadline came by.  One quick vignette:  In an early class, we talk about supermarket affinity cards and how much information you give supermarkets about yourself when you use their cards.  I point out that in return for that information, supermarkets give you discounts and perhaps can better tune their advertising efforts to your individual interests.  Of course, this can work against you:  if a supermarket believes that you will certainly buy a particular salsa, do you think they will give you a coupon for that salsa?  Should they give you such a coupon?  Since their actions are unclear, it is uncertain whether they are helping or hurting you with the information you give them.

That night, we got an automated call from our local supermarket saying that some hash browns we bought a few months ago were tainted with listeria (my wife’s response: “You cook once a month and even then you poison us!”).  They knew we bought the hash browns from the affinity card data, showing an advantage for using the card and providing correct contact data.

The other course I am involved with is Operations Research Implementations.  Our goal in this MBA course is to get way beyond the “four variable, three constraint” formulations and to get students doing things that look more like real-world projects.  We were lucky had had 20 students sign up, which is an ideal size for this type of course.  We chose AIMMS as our modeling package, with Gurobi as the underlying software. I am co-teaching this course with Willem van Hoeve. My main goal was to learn how to use AIMMS, and it has gone very well so far.  I also continue to be very impressed with the Gurobi solver.

For this course, students do a project (in teams), either from us or chosen on their own.  The ones we offered were

  1. Truck contracting (ala work I did with the postal service)
  2. Sports scheduling for a purpose-built little league complex
  3. Inbound distribution routing
  4. Wildlife corridor design

One group has already decided to do a project on their own:  ad placement in an online environment.  We’ll see whether other groups have their own ideas of if they are going to pick from the above).

More later on about doing academic administration, journal activities, and all the other things faculty members do.

Algorithmic Voting Theory, Venice, and a Talk on Old/New Papers

I just got back from Venice, where I attended a conference on Algorithmic Decision Theory.  This is a new conference series (optimistically numbered the first conference, implying at least a second) revolving around issues in uncertainty in decision making, preference solicitation, learning and other issues.  From the conference web page:

A new unique event aiming to put together researchers and practitioners coming from different fields such as Decision Theory, Discrete Mathematics, Theoretical Computer Science and Artificial Intelligence in order to improve decision support in the presence of massive data bases, combinatorial structures, partial and/or uncertain information and distributed, possibly inter-operating decision makers. Such problems arise in several real-world decision making problems such as humanitarian logistics, epidemiology, risk assessment and management, e-government, electronic commerce, and the implementation of recommender systems.

This area has been very active, particularly in computer science where there are  a host of applications.

I was asked to give one of the invited talks, and spoke on “An Operations Research Look at Voting”.  I was a little worried about giving this talk, since my main qualifications come from papers published twenty years ago.  When I was a doctoral student at Georgia Tech, I worked with John Bartholdi and Craig Tovey on computational issues in voting.  Being the first to look at those issues, we got to prove some of the basic results in the area.  These include

  1. For some natural voting rules, it is NP-hard to determine who the winner is.
  2. For some natural voting rules, it is NP-hard to determine how to manipulate the rule (where manipulation means misrepresenting your preferences so as to get a preferred outcome).
  3. For some natural voting rules, optimally using the powers of a chair to form subcommittees or otherwise manipulate the voting process is NP-hard.

We published this work in Social Choice and Welfare (after getting it rejected from more mainstream economics journals) where … it was soundly ignored for 15 years.  No one referred to the papers; no one followed up on the papers;  no one cared about the papers at all!

This work was my job talk in 1987/88, and it got me a wonderful job here at the Tepper School (then GSIA), Carnegie Mellon.  And, without Google Scholar, it was not obvious that the papers were being ignored, so they added to my vita, and made it a bit easier to pass through the various steps.

But I did like the work a lot, and regretted (and still regret) that my economist colleagues did not take computational limits more seriously in their models.

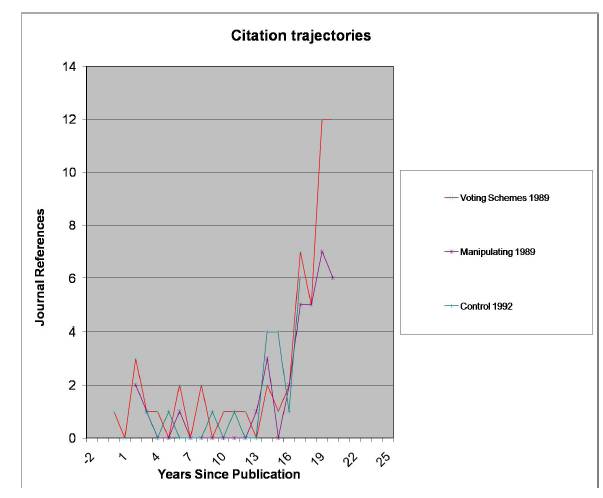votingcitesBut then something amazing happened about 5 years ago:  people started referring to the papers!  The references were mainly in computer science, but at least the papers were being recognized. The counts of these papers in the Web of Science (formerly Science Citation Index) are particularly striking.  In the associated graph, the x-axis is years since publication;  the y-axis is the number of references in Web of Science in that year (Google scholar numbers are higher of course, but there is a bias towards more recent papers there).  In my talk, I compare that graph to my “normal” papers, which reach a peak after 4 or 5 years then decrease.   It is really gratifying to see the interest in these papers along with all the really cool new results people are getting.

I closed off the talk with some work I have done recently on creating voting trees.  Suppose there are three candidates, “a”, “b”, and “c”, and you really like candidate “a”.  Many voting systems proceed as a series of comparisons between two alternatives (think of standard parliamentary procedure).  If you are the chairperson, you might try to bring the candidates forward so as to increase the chances of “a” winning.  In fact, if you set the agenda to be “b” against “c” and the winner against “a”, then “a” will win as long as “a” beats someone (and no one beats everyone).  In this problem, the goal is to do the manipulation without knowing other voters’ preferences.

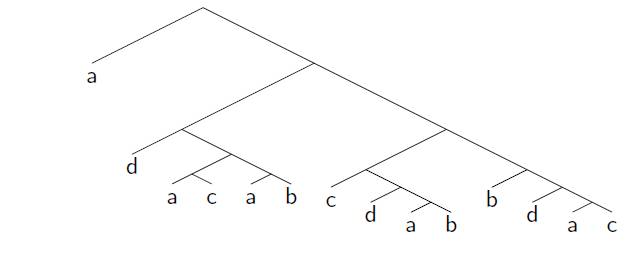lextree4Can you do this for four candidates?  If you want “a” to win, “a” must be in the top cycle: the group of candidates (perhaps the entire set of candidates) who all beat all the other candidates.  The “Condorcet winner” is the minimal top cycle:  if some candidate beats all the other candidates one-on-one, then that candidate must win any voting tree it occurs in.  So, assuming “a” is in the top cycle, can you create a voting  tree so that “a” wins with four candidates?  The answer is yes, but it is a bit complicated:  first “a” goes against “c” with the winner against “d” then the winner against “b” who plays the winner of (“a” goes against “b” with the winner against “d” …) ….  actually, the minimum tree has 14 leaves!  I am biased, but I think the tree is beautiful, but it goes to show how hard it is to manipulate agendas without knowledge of others’ preferences.  I am in the process of generating the trees on 4 candidates:  there is a very natural rule (“Copeland winner with Copeland loser tie break”:  see the presentation for definitions) that requires more than 32 leaves (if an implementation tree for it exists).

Sanjay Srivastava and I made a conjecture almost 15 years ago that would imply that this sort of manipulation would be possible no matter how many candidates.  Little progress has been made but I think it is still a great problem (the economists know this as implementation by backwards induction and characterizing rules implementable on trees is an important problem in social choice/mechanism design).

If you want more details on all this, here are my slides.  The references are

  • Small Binary Voting Trees M.A. Trick, Small Binary Voting Trees, First International Workshop on Computational Social Choice,
    Amsterdam, Netherlands, 500-511 (2006).
  • Sophisticated Voting Rules S. Srivastava and M.A. Trick, Sophisticated voting rules: The two tournament case, Social Choice and
    Welfare, 13: 275-289 (1996).
  • How hard is it to control an election?, with C. A. Tovey and M. A. Trick. A slightly revised version of this appeared in Mathl. Comput. Modelling (Special Issue on Formal Theories of Politics) 16(8/9):27-40 (1992).
  • The computational difficulty of manipulating an election, J.J. Bartholdi, C. A. Tovey and M. A. Trick (1989); Social Choice and Welfare 6:227-241 (1989).
  • Voting schemes for which it can be difficult to tell who won the election, J.J. Bartholdi, C. A. Tovey and M. A. Trick; Social Choice and Welfare 6:157-165 (1989).

Oh, and Venice is a beautiful place to visit.  But you might have heard that elsewhere.